Оглавление:
Интегрирование рациональных дробей
Рациональной дробью называется отношение двух многочленов:
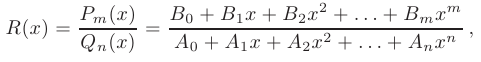
где 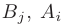 — заданные коэффициенты. Рациональная дробь называется правильной, если
— заданные коэффициенты. Рациональная дробь называется правильной, если 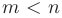 и неправильной, если
и неправильной, если 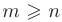 .
.
Интегрирование простейших рациональных дробей. Различают 4 типа простейших рациональных дробей:
- Интегрирование простейшей рациональной дроби I типа выполняется по формуле:
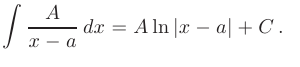
Интегрирование простейшей рациональной дроби II типа выполняется по формуле:
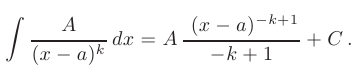
Интегрирование простейшей рациональной дроби III типа
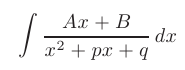
уже было описано в предыдущем разделе.
- Интегрирование простейшей рациональной дроби IV типа
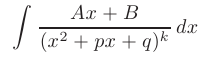
описано в рекомендуемой литературе (см. соответствующие разделы в |1, 3, 6]).
Заметим, что достаточно рассмотреть лишь правильные дроби, так как любую неправильную дробь можно представить в виде суммы многочлена 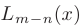 и правильной дроби, используя алгоритм деления многочленов «уголком». Полученный при этом интеграл
и правильной дроби, используя алгоритм деления многочленов «уголком». Полученный при этом интеграл 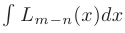 вычисляется методом разложения.
вычисляется методом разложения.
Чтобы вычислить интеграл от правильной рациональной дроби подынтегральную функцию нужно представить в виде простейших рациональных дробей и проинтегрировать по отдельности.
Для этого знаменатель дроби должен быть представлен в виде произведения линейных и (или) квадратичных множителей, например:
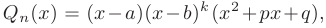
где 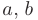 — корни многочлена,
— корни многочлена, 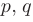 — известные действительные числа, трехчлен
— известные действительные числа, трехчлен 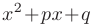 не имеет действительных корней, а
не имеет действительных корней, а 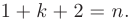
Тогда дробь
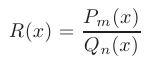
представляется в виде суммы простейших дробей:
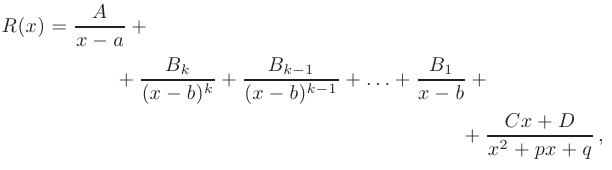
где 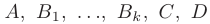 — неизвестные коэффициенты, которые находятся путем приведения суммы справа к общему знаменателю и последующего приравнивания полученного числителя к
— неизвестные коэффициенты, которые находятся путем приведения суммы справа к общему знаменателю и последующего приравнивания полученного числителя к 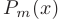 .
.
Пример:
Найти неопределенный интеграл методом разложения рациональной дроби на простейшие
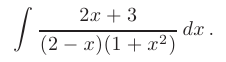
► Для интегрирования правильной рациональной дроби выполним вначале ее разложение на простейшие методом неопределенных коэффициентов. С учетом множителей, стоящих в знаменателе исходной дроби, ее разложение будет содержать простейшие дроби I и III типов:
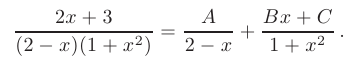
Для нахождения неопределенных коэффициентов выполним сложение простейших дробей и проведем группировку полученного числителя по степеням переменной 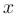 :
:
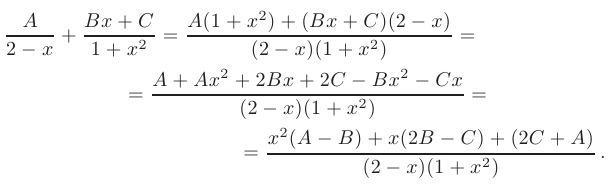
Из равенства заданной и полученной дробей с одинаковыми знаменателями следует равенство их числителей:
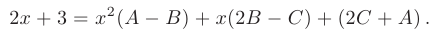
Приравняв коэффициенты при одинаковых степенях 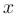 , составим систему уравнений относительно неопределенных коэффициентов
, составим систему уравнений относительно неопределенных коэффициентов 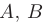 и
и 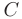 :
:
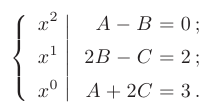
Решив полученную систему, найдем значения неопределенных коэффициентов:
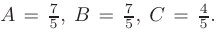
Тогда искомое разложение примет вид
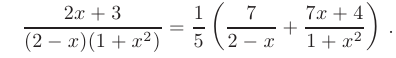
Используя полученное разложение, исходный интеграл может быть записан в виде суммы интегралов от простейших рациональных дробей
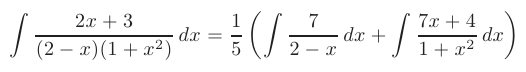
Интегрирование простейшей рациональной дроби I типа легко выполняется после замены переменной 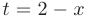 :
:
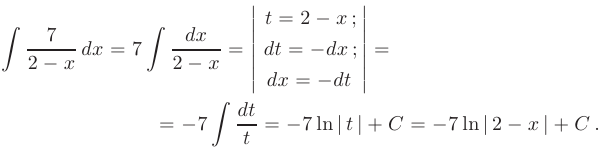
Для интегрирования простейшей рациональной дроби III типа запишем интеграл в виде суммы двух интегралов:
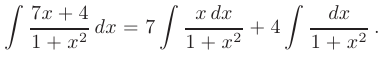
Второе слагаемое представляет собой табличный интеграл (см. приложение В.12)
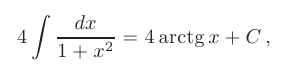
а первое слагаемое легко приводится к табличному виду с помощью замены переменной 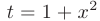 :
:
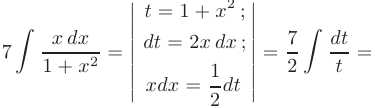
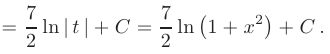
Объединяя полученные результаты, искомый интеграл можно записать в виде:
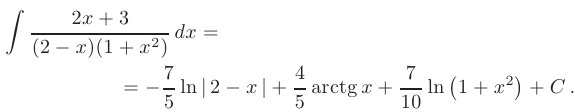
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Основные методы интегрирования в математике |
| Интегрирование некоторых классов функций в математике |
| Интегрирование иррациональных функций в математике |
| Понятие определенного интеграла в математике |

