Интегрирование рациональных дробей

Интегрирование простейших рациональных дробей

Найдем интегралы от простейших рациональных дробей.

1. (формула (2) таблицы интегралов);

2. (формула (1));

3. Рассмотрим интеграл .

Выделив в знаменателе полный квадрат, получим:

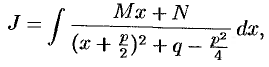
причем . Сделаем подстановку . Тогда , . Положим 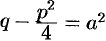. Следовательно, используя формулы (2) и (15) таблицы интегралов, получаем

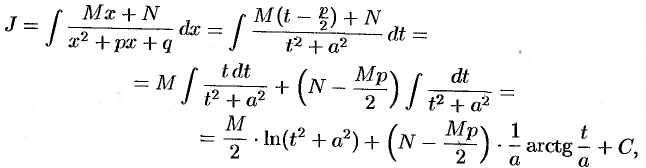
т. e., возвращаясь к переменной ,

Пример №31.5.

Найти .

Решение:

. Сделаем подстановку 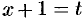. Тогда 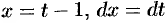и

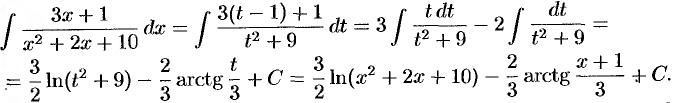
4. Вычисление интеграла вида .

Данный интеграл подстановкой сводится к сумме двух интегралов:

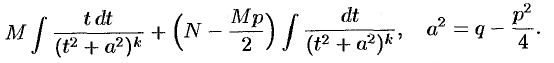
Первый интеграл легко вычисляется:

Вычислим второй интеграл:

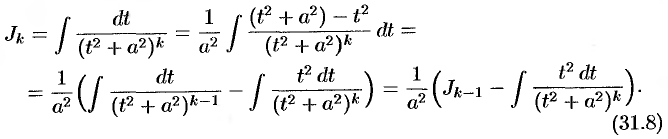
К последнему интегралу применим интегрирование по частям. Положим

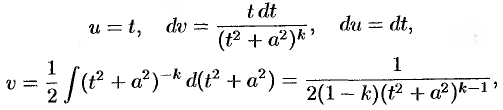
тогда

Подставляя найденный интеграл в равенство (31.8), получаем

т. е.

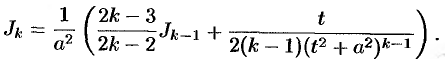
Полученная формула дает возможность найти интеграл для любого натурального числа .

Дополнительный пример №31.6.

Интегрирование рациональных дробей

Рассмотренный в пунктах 31.1-31.2 материал позволяет сформулировать общее правило интегрирования рациональных дробей.

1. Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби;
2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей;
3. Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример №31.7.

Найти интеграл .

Решение:

Под знаком интеграла неправильная дробь; выделим ее целую часть путем деления числителя на знаменатель:

Получаем:

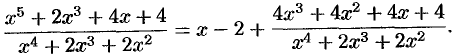
Разложим правильную рациональную дробь на простейшие дроби:

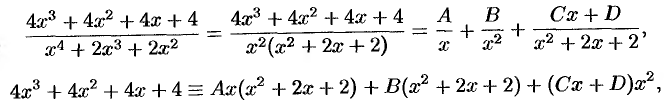
т. е.

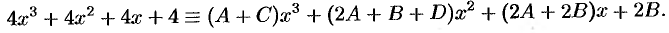
Отсюда следует, что

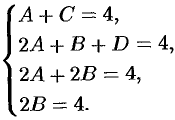
Находим: . Стало быть,

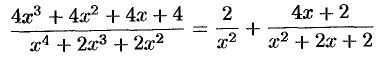
и

Интегрируем полученное равенство:

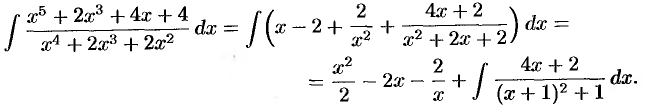
Обозначим 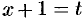, тогда и . Таким образом,

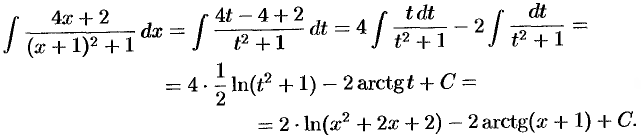
Следовательно,

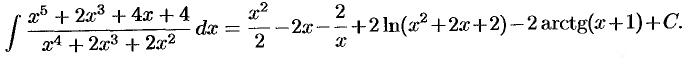
Отметим, что любая рациональная функция интегрируется в элементарных функциях.

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Понятия о рациональных функциях

Дробно-рациональная функция

Универсальная тригонометрическая подстановка

Интегралы типа sin m x cos n x dx