Оглавление:
Интегрирование простейших рациональных дробей
Всякую рациональную функцию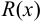 
можно представить в виде отношения двух многочленов: 
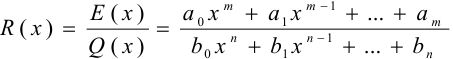, причём
многочлены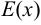 
и 
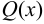общих корней не имеют.
Если степень многочлена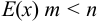 
, то дробь правильная, если 
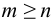, то дробь неправильная. При помощи деления неправильную рациональную дробь можно представить в виде суммы целой рациональной функции (целой части) и правильной рациональной дроби.
Пусть 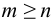, тогда
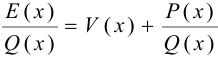, где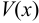 
— целая рациональная функция, а 
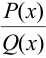— правильная рациональная дробь.
Теорема. Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей следующих типов:
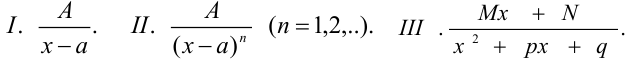
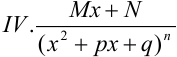, где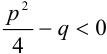 
, т. е. корни знаменателя мнимые.
Простейшие дроби I и II типов интегрируются следующим образом:
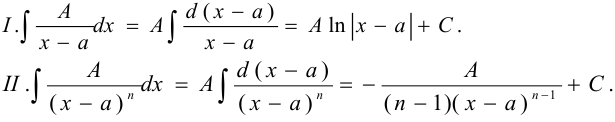
Задача №80.
Вычислить интеграл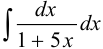 
.
Решение:
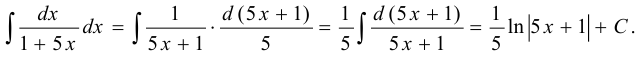
Простейшая дробь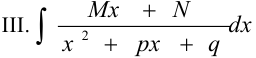 
интегрируется следующим образом. В знаменателе выделяем полный квадрат: 
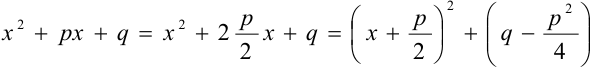и делаем подстановку 
.
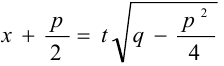Имеем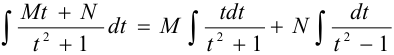 
.
Задача №81.
Вычислить интеграл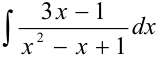 
.
Решение:
В знаменателе подынтегральной функции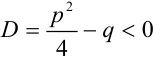 
, следовательно, интегрируется простейшая дробь третьего типа III:
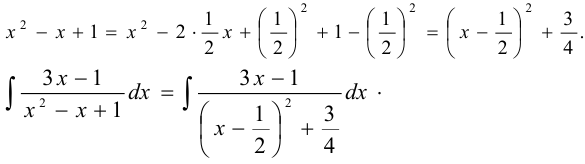
Делаем замену: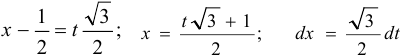 
.
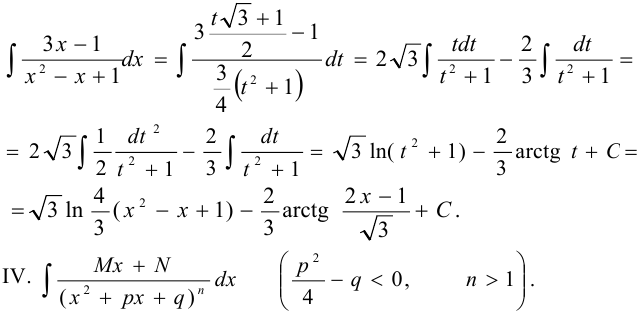
В интеграле этого типа выделяют в знаменателе полный квадрат:
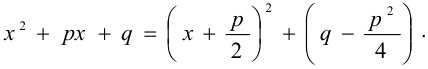
Подстановкой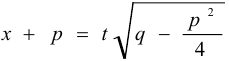 
— приводят интеграл к виду
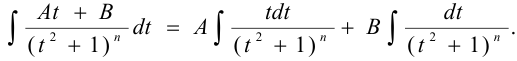
Первый интеграл в правой части легко приводится к табличному, а второй — находится с помощью рекуррентной формулы, полученной при решении задачи.
Задача №82.
Вычислить интеграл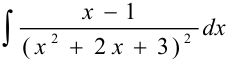 
.
Решение:
В знаменателе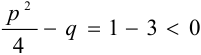 
, следовательно, интегрируется простейшая дробь четвёртого типа IV.
Выделим полный квадрат в знаменателе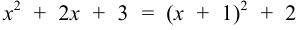 
. Сделаем подстановку 
, 
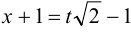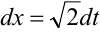, тогда
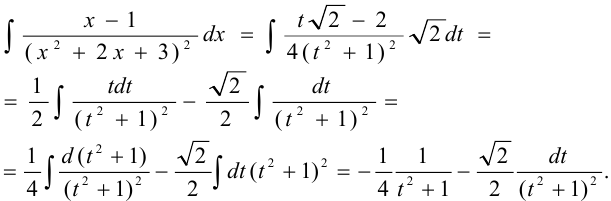
Известна такая рекуррентная формула для интеграла:
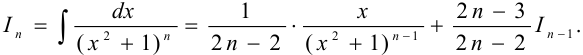
Для нашего случая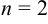 
, отсюда имеем
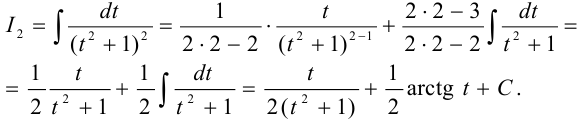
Подставим в наше выражение:
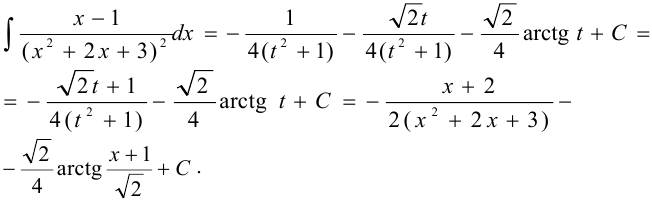
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
