Всего различают 4 типа простейших рациональных дробей:
1. Простейшая дробь 1-го типа имеет вид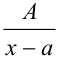 
, где 
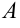— коэффициент, 
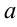— действительный корень знаменателя. Интеграл от дроби 1-го типа приводится к табличному интегралу:
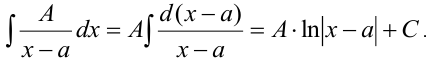
2. Простейшая дробь 2-го типа имеет вид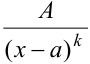 
, где 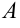— коэффициент, 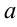— действительный корень знаменателя кратности 
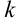. Интеграл от дроби 2-го типа приводится к табличному интегралу:
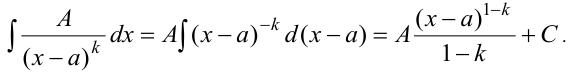
3. Простейшая дробь 3-го типа имеет вид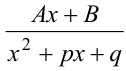 
, где , 
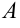— коэффициенты, знаменатель дроби не имеет действительных корней, его дискриминант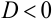 
.
При интегрировании дроби вначале в числителе нужно выделить дифференциал знаменателя (если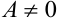 
).
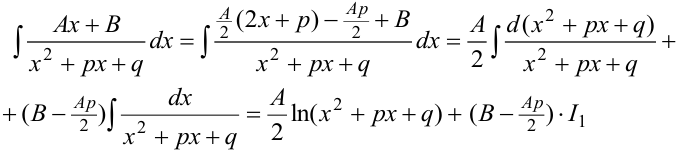
Интеграл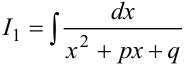 
превращается в табличный, если в знаменателе выделить полный квадрат суммы или разности и применить подстановку 
.
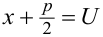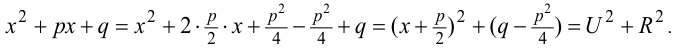
Так как дискриминант знаменателя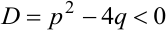 
, то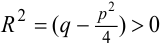 
.
Таким образом,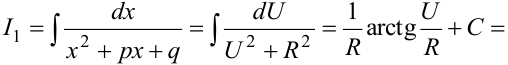 
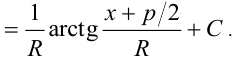
Пример:
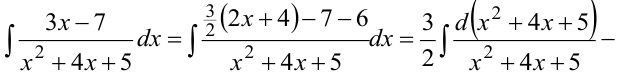
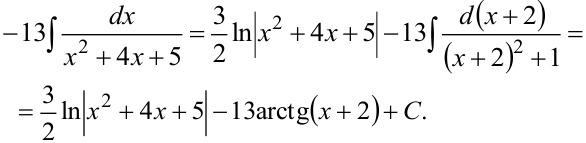
Использованы табличные интегралы №2 и №15.
Примечание — если знаменатель дроби 3-го типа имеет действительные корни, то дробь не считается простейшей. Однако и в этом случае можно применять рассмотренный способ интегрирования.
4. Простейшая дробь 4-го типа имеет вид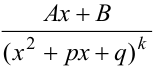 
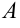, где , — коэффициенты, знаменатель дроби не имеет действительных корней, его дискриминант 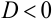. Называясь «простейшей», дробь интегрируется весьма непросто. Интегрирование таких дробей см. в пособии.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Интегрирование по частям |
| Интегрирование подстановкой |
| Разложение многочлена на множители |
| Разложение рациональной дроби на сумму элементарных дробей |
