Оглавление:
При вычислении определенных интегралов широко используется метод замены переменной. Пусть требуется вычислить интеграл от сложной функции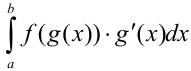 
. Как и для неопределенного интеграла, сделаем подстановку 
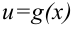. Тогда 
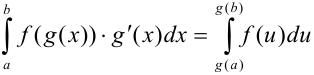. Эта формула называется формулой замены переменной в определенном интеграле.
Алгоритм вычисления определенных интегралов методом замены переменной практически не отличается от алгоритма метода замены переменной для неопределенных интегралов (лекция 19). Отметим два принципиальных различия:
- В определенном интеграле обязательной является смена границ интегрирования. Новая нижняя граница интегрирования будет равна
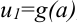, а новая верхняя граница 
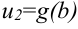. - При вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется.
Рассмотрим применение метода замены переменной в определенном интеграле.
Пример №22.2.
Вычислите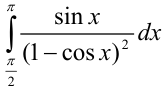 
.
Решение:
1. Выполним подстановку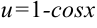 
с целью прийти к интегралу от функции 
.
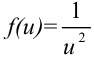2. Найдем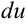 
по формуле 
: 
.
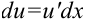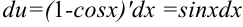3. Выразим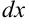 
из выражения пункта 2 (
): 
.
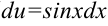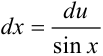4. Подставим 
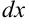и в исходный интеграл (пока неопределенный): 
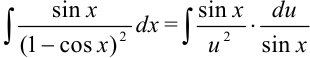. Видим, что 
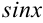можно сократить и прийти к интегралу относительно переменной : 
.
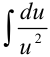5. Вычислим новые границы интегрирования для переменной . Для этого подставим существующие границы (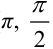
) в выражение 
.
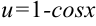Тогда нижняя граница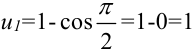 
; верхняя граница 
.
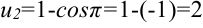В результате всех преобразований первоначальный интеграл примет вид: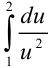 
.
6. Вычислим полученный интеграл. По таблице интегралов находим, что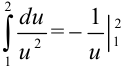 
. Воспользуемся свойством 3 определенного интеграла, позволяющим менять границы интегрирования, при этом избавляясь от знака «минус» перед определенным интегралом 
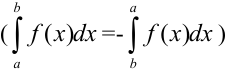. Тогда 
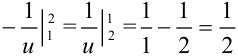. Еще раз отметим, что к переменной 
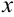после смены границ интегрирования возвращаться не нужно!
Ответ: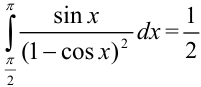 
.
Пример №22.3.
Вычислите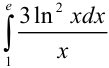 
.
Решение:
1. Выполним подстановку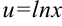 
с целью прийти к интегралу от функции 
.
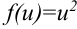2. Найдем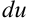 
по формуле 
: 
.
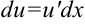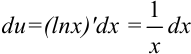3. Выразим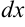 
из выражения пункта 2 (
): 
.
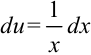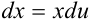4. Подставим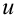 
и 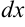в исходный интеграл (пока неопределенный): 
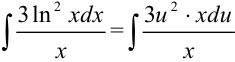. Видим, что 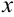можно сократить и прийти к интегралу относительно переменной : 
.
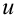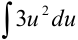5. Вычислим новые границы интегрирования для переменной 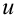. Для этого подставим существующие границы (1, 
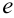) в выражение .
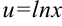Тогда нижняя граница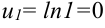 
; верхняя граница 
.
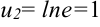В результате всех преобразований первоначальный интеграл примет вид: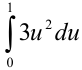 
.
6. Вычислим полученный интеграл: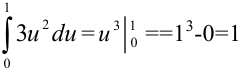 
.
Ответ: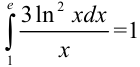 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Формула Ньютона-Лейбница. |
| Применение формулы Ньютона-Лейбница. |
| Интегрирование по частям. |
| Геометрический смысл определенного интеграла |
