Формула интегрирования по частям для определенного интеграла практически не отличается от аналогичной формулы для неопределенного интеграла, только добавляются границы интегрирования: 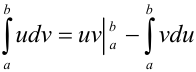 .
.
Рекомендации по выбору 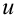 и
и 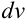 , а также алгоритм нахождения интеграла методом по частям были подробно разобраны в лекции 19. Рассмотрим примеры применения метода интегрирования по частям в определенном интеграле.
, а также алгоритм нахождения интеграла методом по частям были подробно разобраны в лекции 19. Рассмотрим примеры применения метода интегрирования по частям в определенном интеграле.
Пример №22.4.
Найдите 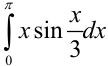 .
.
Решение:
1. Исходный интеграл имеет вид 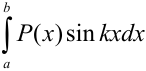 , следовательно, за
, следовательно, за 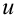 принимают многочлен (
принимают многочлен (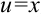 ), остальные множители — за
), остальные множители — за 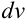 :
: 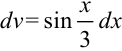 .
.
2. Находим 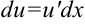 :
: 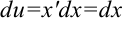 .
.
Находим 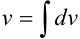 :
: 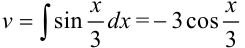 (интеграл от некоторой сложной функции, полагаем
(интеграл от некоторой сложной функции, полагаем 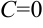 ).
).
3. По формуле 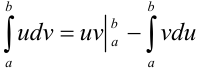 имеем:
имеем: 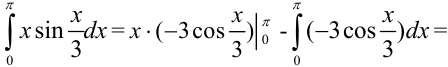
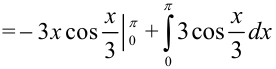 . Вычислим каждое слагаемое выражения отдельно:
. Вычислим каждое слагаемое выражения отдельно:
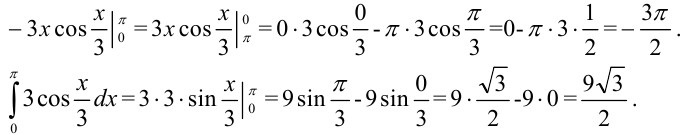
Тогда исходный интеграл равен 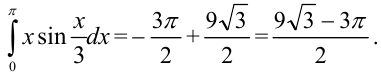
Ответ: 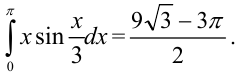
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:

