Оглавление:
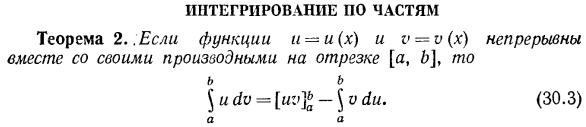




Интегрирование по частям
Интегрирование по частям. Теорема 2..Если функции u = u (x) и o = u (x) непрерывны с производными интервала[a, b、 Эта формула называется интегральной формулой для каждой части конкретного интеграла. Доказательство. Есть Поскольку подынтегральная функция непрерывна, все эти интегралы существуют. Но согласно формуле Ньютона Лейбница Если сравнить формулы (30.4) и (30.5), то получим равенство Отсюда следует формула (30.3). Тс Определите эти функции.
Теорема 2 может быть легко обобщена в случае так называемых кусочно-непрерывных дифференцируемых функций. Людмила Фирмаль
- Если мы определим функцию [(x) в отрезке[a, b], то разбиение m = {x, -} 1 = o в отрезке[a, b]существует, f (x) равно каждому интервалу (x, −1, x.) и конечным пределам f (x, _1 + 0), f (x, −00), r = 1, 2…, k существует (следовательно, функция / относится к интервалу[a, B],§ 28.3 определение 1.As упомянутое выше (см. доказательство теоремы 28.3 из 2), введем функцию Определение 1.Каждая функция f, (x), r = 1, 2,…к、 Если интервал дифференцируем, то функция [(x) называется кусочно (непрерывно) дифференцируемой по интервалу[a, b]. Теорема 2 ’.Предположим, что функции u (x) и V (x) непрерывны и кусочно дифференцируемы на интервале[a, b\, и что
- Формула для интегрирования по частям (30.3) справедлива. Доказательство теоремы 2 также справедливо в этом case. In дело в том, что произведение m непрерывно и его производная (io) ’= io ’ + u! O кусочно непрерывна. Таким образом, согласно теореме 5 29.2-клаузула, формула Ньютона-Лейбница также может быть применена к интегралу в левой части(30.5). Ноль Образцы. 1.Найти значение Интеграла§ 1пхйх. Пожалуйста, обратите внимание Он является частью интегрированной формулы. 2.Любое n = 0, 1, 2,…Против、 Прежде всего, заметим, что уравнение Интеграла(30.7) можно легко установить, заменив переменную x = l / 2-I. In кроме того, вы получаете Интеграл для каждой части.
Благодаря определению, первое из этих равенств также означает справедливость формулы Уоллиса. Людмила Фирмаль
- Обратите внимание, что 70 = ^ xx -^, / 1 = ^ zxxx = 1.И так оно и есть.、 n-2k + 1, то есть нечетное、 И если n = 2k, то это дажеИз Формулы (30.7) можно легко получить так называемую формулу Уоллиса**.Это будет необходимо в будущем. * «Клянусь Я!!, Л), i 1-произведение всех натуральных чисел, не превышающих n и имеющих ту же четность, что и I. * * J. Уоллис (1616-1703) английский математик、 Мы это докажем. Интеграция неравенства Вдоль интервала[0, Pi/ 2]、 (На самом деле легко показать, что существует строгое неравенство.) Благодаря (30.7) Благодаря этому неравенству поскольку M» ω, то η (yn-xn)= 0, то есть длина отрезка[xn, yn]π / 2 Потому что она стремится к нулю、 Тс Упражнение. Вычислите определенный интеграл.
Смотрите также:
| Формула Ньютона-Лейбница. | Вторая теорема о среднем значении для определенного интеграла. |
| Замена переменной. | Интегралы от вектор-функций. |

