Оглавление:
Интегрирование нормальных систем
Одним из основных методов интегрирования нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. (Обратная задача — переход от ДУ к системе — рассмотрена выше на примере.) Техника этого метода основана на следующих соображениях.
Пусть задана нормальная система (52.1). Продифференцируем по  любое, например первое, уравнение:
любое, например первое, уравнение:
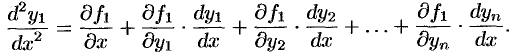
Подставив в это равенство значения производных 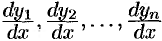 из системы (52.1), получим
из системы (52.1), получим
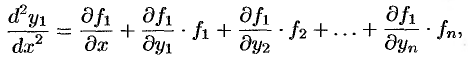
или, коротко,
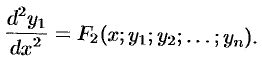
Продифференцировав полученное равенство еще раз и заменив значения производных 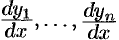 из системы (52.1), получим
из системы (52.1), получим
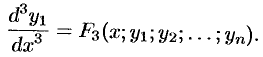
Продолжая этот процесс (дифференцируем — подставляем — получаем), находим:
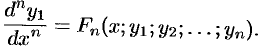
Соберем полученные уравнения в систему:
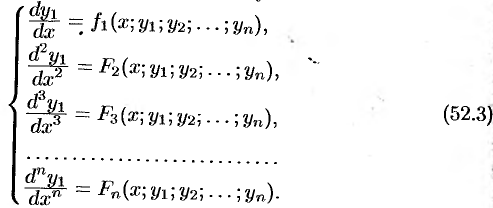
Из первых 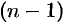 уравнений системы (52.3) выразим функции
уравнений системы (52.3) выразим функции 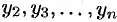 через
через  , функцию
, функцию 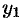 и ее производные
и ее производные 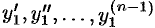 . Получим
. Получим
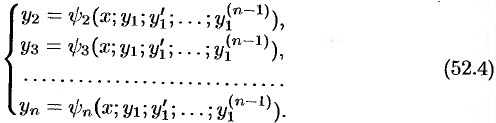
Найденные значения 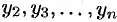 подставим в последнее уравнение системы (52.3). Получим одно ДУ
подставим в последнее уравнение системы (52.3). Получим одно ДУ  -го порядка относительно искомой функции
-го порядка относительно искомой функции 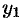 :
: 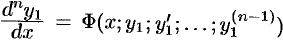 . Пусть его общее решение есть
. Пусть его общее решение есть
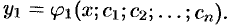
Продифференцировав его 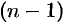 раз и подставив значения производных
раз и подставив значения производных 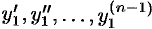 в уравнения системы (52.4), найдем функции
в уравнения системы (52.4), найдем функции 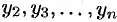 :
:
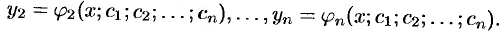
Пример №52.1.
Решить систему уравнений
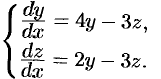
Решение:
Продифференцируем первое уравнение: 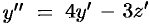 . Подставляем
. Подставляем 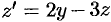 в полученное равенство:
в полученное равенство: 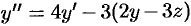 ,
, 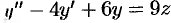 . Составляем систему уравнений:
. Составляем систему уравнений:
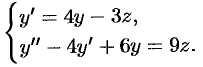
Из первого уравнения системы выражаем  через
через  и
и 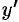 :
:

Подставляем значение  во второе уравнение последней системы:
во второе уравнение последней системы:
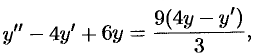
т. е.  . Получили одно ЛОДУ второго порядка. Решаем его:
. Получили одно ЛОДУ второго порядка. Решаем его: 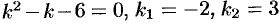 и
и 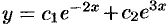 — общее решение уравнения. Находим функцию
— общее решение уравнения. Находим функцию  . Значения
. Значения  и
и 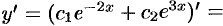
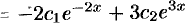 подставляем в выражение
подставляем в выражение  через
через  и
и 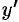 (формула (52.5)). Получим:
(формула (52.5)). Получим:
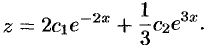
Таким образом, общее решение данной системы уравнений имеет вид 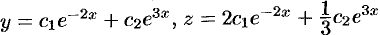 .
.
Замечание. Систему уравнений (52.1) можно решать методом интегрируемых комбинаций. Суть метода состоит в том, что посредством арифметических операций из уравнений данной системы образуют так называемые интегрируемые комбинации, т. е. легко интегрируемые уравнения относительно новой неизвестной функции.
Проиллюстрируем технику этого метода на следующем примере.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Структура общего решения ЛНДУ второго порядка |
| Метод вариации произвольных постоянных ЛНДУ |
| Ряд геометрической прогрессии |
| Необходимый признак сходимости числового ряда |

