Оглавление:




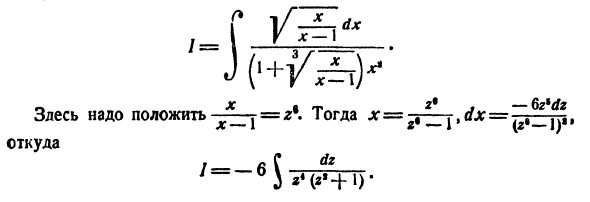

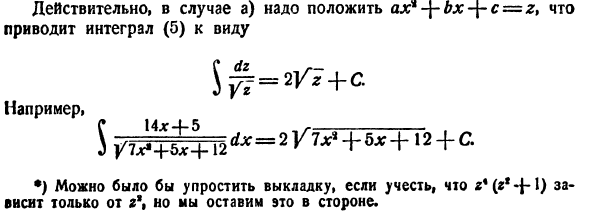

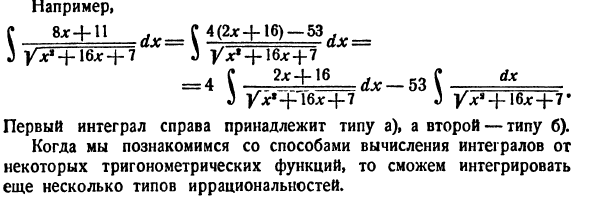

Интегрирование некоторых иррациональностей
Интеграция некоторой иррациональности № 1. Рационализация подынтегральных функций. В отличие от рациональных функций, иррациональные выражения всегда далеки от интеграции в основные функции. В этом разделе рассматриваются некоторые конкретные типы иррациональных функций, которые интегрируются в конечной форме.
- Во многих случаях интегрирование иррациональных функций может быть выполнено путем сокращения этой функции путем замены ее рациональной функцией. Суть метода * впервые показана на примере. Дай мне Вермонт дх. * ‘+ * z-1 • -g -2-1 Вот так 1 Th + V7T Установка x = z находит dx = 2zdz. г C 2 * F L O C Мы решили консолидировать разумную пропорцию. Поскольку дробь неверна, разделите числитель на знаменатель (с остатком):
Этот метод называется рационализацией подынтегрального выражения, а упомянутая замена называется рационализационной заменой. Людмила Фирмаль
Оптимизированная функция частичной интеграции Вернитесь к старой переменной x и замените z на Yx. в конце концов / == * -2VT + 2In (V * 4- + С- ^ Подобная интеграция ***, _Сtf * J1 + V * Упорядоченная форма подстановки — jcssz «, потому что * существует только под корнем куба. S Sqnf— • S 1 * [5-x + s ^ + D] + c; Откуда Для интеграции ситуация сложнее
Использовать vldx В конце концов, здесь x появляется в знаках квадратного и кубического корней. Естественно поставить x = z \ так, чтобы оба этих маршрута были извлечены Откуда / == 6 (T-7 + S— * + «rctg») + C
Замена z на fx остается. Анализ этих примеров показывает следующее: Правила. f (u, v, w, …) — рациональная функция аргумента ♦) и a, a, p, … — натуральные числа, Тогда интегрируйте \ f {x, V *, V *, ..) dx (® •) То есть не нужно выполнять никаких действий, кроме арифметических (например, f), чтобы найти f (ut v, w, …) в этих аргументах. u * + 2uv
- Свести к интегралу рациональной функции, заменив х = зН Где N — наименьшее общее кратное корневого индекса a и b% Фактически, в результате подстановки (2) все корни интеграла извлекаются . Подобные перестановки упрощают объединение с более общими интегралами \ f {> V ^ H) • «/ {M + 5T (3) Где f — рациональное число, a, b, a, p, … — целые числа, a / C »L P, Q — постоянная.
Точно должен быть поставлен здесь (4) Kx + L_ N Где H — наименьшее общее кратное корневых индексов a и b *, как описано выше. Интеграл (3) равен (1>, когда К = 1 »1 = 0, = = 0 и Q = 1. (4) затем переходит к (2). Мы объясняем, что было сказано в двух примерах. 1) _ Установите x — \ — \ = z \ dx = 2zdzt 2) Найти другой интеграл (2) \ дх J F L-I X 2 * _6z * £ fz Здесь вы должны поставить = * • x == z * ^ пгур » Откуда = J
*) 1 _ A, B C, D, Ez + F от r * (r * + ) до ‘z «» 2 F + T • Отсюда Предполагая, что 2 = 0, A = 1. Сравнение степеней z дает пять уравнений. 0 = D + E, 24 0 = C + F, 0 = L l> 0 = l + s, Z 0 = I Так что B = D = E = 0, C = -1 и F = 1. Таким образом, № 2. Интегральный ^ интегральный расчет Эта форма напоминает интегральные (20) §1 вычисления.
Интеграл f Ax + B _ dx J Vax * -f bx -f с Фракция g4 ij разбивается на простые дроби по схеме Людмила Фирмаль
То есть интегральная C Ah + B \ Vox> + bx + c dx <5> Он рассчитывается без каких-либо проблем в следующих двух случаях. а) Числитель Ax — \ — B является радикальной производной троичного ax1 + bx + c. б) Числитель не зависит от х. То есть А = 0.
Действительно, случай a) ajc * + bx + c = z должен быть помещен. Это дает интеграл (5) вида Например S y 7 L £ + 12 ‘** ■ -2 V ™ — + до +’ 2 + C •) Учитывая, что это зависит только от r * (r * — \ — ), можно упростить расчет, но проигнорировать его.
В случае б) необходимо извлечь полный квадрат из корневой тройки. Это приводит к интегралу в X или XIII, в зависимости от знака a. Например j_Сdx_Сdx_ Y-3.x ‘+ \ bx + 2 J} / -3 (> — 6lg + 9) +29′ Отсюда / = [= = 1 [^ 1/3 (дг-3) | J / 29-3 (x-3) — / 3 J / 29-3 (x-3) «и, наконец, Я — Смола ^ < Г3> + С. Галстук с 29 я
Точно так же, / = L дх J yx + + bx + r J y3 (x «+ 6jc + 9) -25 ‘ Отсюда , 1 C tf [/ T (.r + 3) i = / J J / 3 (X + 3) до -25 = 7Г1п ^ + 3) + VW + lSx + 2] + C. Наконец, если вы разделите числитель Ax — \ — B на троичную производную 2ax — \ — L и запишите Ax — \ — B в качестве делителя, умноженного на частное и остаток, общий случай интегрирования (5) будет Можно свести к случаям а) и б).
J U * * + 6x + 7 = 4 [* ± X ± _ix-Ui J Ux9 + \ 6x + 1 J б / лг Yx ‘+ \ 6x + T Первый интеграл справа принадлежит типу а), а второй принадлежит типу б). По мере того, как вы становитесь более привыкшими к вычислению интеграла некоторых тригонометрических функций, вы также можете интегрировать несколько типов иррациональности. Например, 8l- + 11 ух * + \ 6х + 1
Смотрите также:
| Общие приемы интегрирования | Интегрирование некоторых трансцендентных функций |
| Интегрирование рациональных функций | Определение и важнейшие свойства определенного интеграла |

