Оглавление:
Интегрирование ЛОДУ n-го порядка с постоянными коэффициентами
Задача нахождения общего решения ЛОДУ  -го порядка
-го порядка 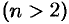 с постоянными коэффициентами
с постоянными коэффициентами
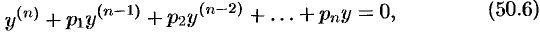
где 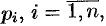 — числа, решается аналогично случаю уравнения вторит порядка с постоянными коэффициентами.
— числа, решается аналогично случаю уравнения вторит порядка с постоянными коэффициентами.
Сформулируем необходимые утверждения и рассмотрим примеры.
Частные решения уравнения (50.6) также ищем в виде 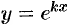 , где
, где 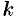 — постоянное число.
— постоянное число.
Характеристическим для уравнения (50.6) является алгебраическое уравнение  -го порядка вида
-го порядка вида
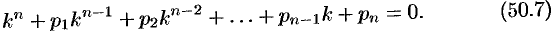
Уравнение (50.7) имеет, как известно,  корней (в их числе могут быть и комплексные). Обозначим их через
корней (в их числе могут быть и комплексные). Обозначим их через 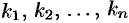 .
.
Замечание. Не все из корней уравнения (50.7) обязаны быть различными. Так, в частности, уравнение 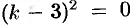 имеет два равных корня:
имеет два равных корня: 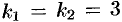 . В этом случае говорят, что корень один
. В этом случае говорят, что корень один  и имеет кратность
и имеет кратность 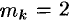 . Если кратность корня равна единице:
. Если кратность корня равна единице: 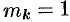 , его называют простым.
, его называют простым.
Случай 1. Все корни уравнения (50.7) действительны и просты (различны). Тогда функции 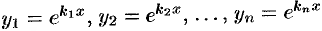 являются частными решениями уравнения (50.6) и образуют фундаментальную систему решений (линейно независимы). Поэтому общее решение уравнения (50.6) записывается в виде
являются частными решениями уравнения (50.6) и образуют фундаментальную систему решений (линейно независимы). Поэтому общее решение уравнения (50.6) записывается в виде
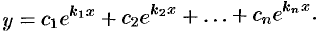
Пример №50.3.
Найти общее решение уравнения
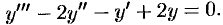
Решение:
Характеристическое уравнение 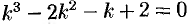 имеет корни
имеет корни 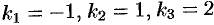 . Следовательно,
. Следовательно, 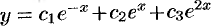 — общее решение данного уравнения.
— общее решение данного уравнения.
Случай 2. Все корни характеристического уравнения действительные, но не все простые (есть корни, имеющие кратность 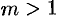 ). Тогда каждому простому корню к соответствует одно частное решение вида
). Тогда каждому простому корню к соответствует одно частное решение вида 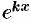 , а каждому корню к кратности
, а каждому корню к кратности 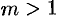 соответствует
соответствует 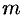 частных решений:
частных решений: 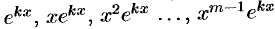 .
.
Пример №50.4.
Решить уравнение 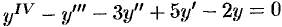 .
.
Решение:
Характеристическое уравнение
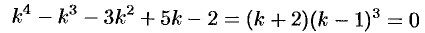
имеет корни 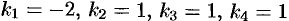 . Следовательно,
. Следовательно,
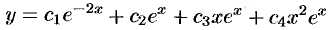
— общее решение уравнения.
Случай 3. Среди корней уравнения (50.7) есть комплексно-сопряженные корни. Тогда каждой паре 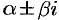 простых комплексно-сопряженных корней соответствует два частных решения
простых комплексно-сопряженных корней соответствует два частных решения 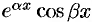 и
и 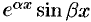 , а каждой паре
, а каждой паре 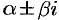 корней кратности
корней кратности 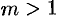 соответствуют
соответствуют 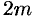 частных решений вида
частных решений вида
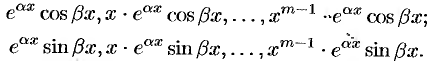
Эти решения, как можно доказать, образуют фундаментальную систему решений.
Пример №50.5.
Решить уравнение 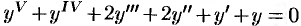 .
.
Решение:
Характеристическое уравнение
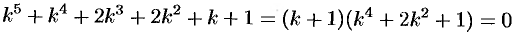
имеет корни 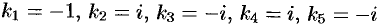 . Следовательно,
. Следовательно,
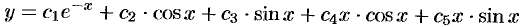
— общее решение уравнения.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

