Оглавление:
Интегрирование ЛНДУ второго порядка с постоянными коэффициентами и правой частью специального вида
Рассмотрим ЛНДУ второго порядка с постоянными коэффициентами, т. е. уравнение
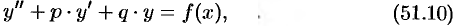
где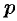 
и 
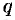— некоторые числа.
Согласно теореме 51.1, общее решение уравнения (51.10) представляет собой сумму общего решения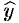 
соответствующего однородного уравнения и частного решения 
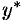неоднородного уравнения. Частное решение уравнения (51.10) может быть найдено методом вариации произвольных постоянных (п. 51.2).
Для уравнений с постоянными коэффициентами (51.10) существует более простой способ нахождения 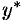, если правая часть 
уравнения (51.10) имеет так называемый «специальный вид»:
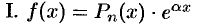
или
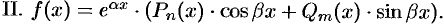
Суть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части уравнения (51.10) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в уравнение (51.10) и из полученного тождества находят значения коэффициентов.
Случай 1. Правая часть (51.10) имеет вид 
, где 
— многочлен степени 
. Уравнение (51.10) запишется в виде
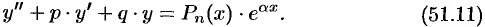
В этом случае частное решение 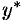ищем в виде:
где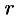 
— число, равное кратности 
как корня характеристического уравнения 
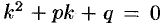(т.е. 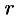— число, показывающее, сколько раз является корнем уравнения 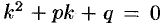), a 
— многочлен степени , записанный с неопределенными коэффициентами 
.
а) Пусть не является корнем характеристического уравнения
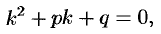
т. е. 
. Следовательно,
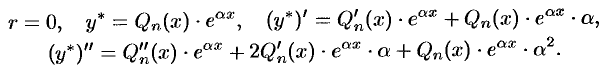
После подстановки функции 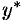и ее производных в уравнение (51.11), сокращения на 
, получим:
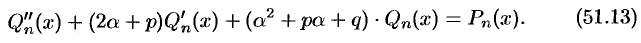
Слева — многочлен степени с неопределенными коэффициентами, справа — многочлен степени , но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях 
, получим систему 
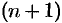алгебраических уравнений для определения коэффициентов 
.
б) Пусть является однократным (простым) корнем характеристического уравнения 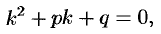, т. е. 
.
В этом случае искать решение в форме 
нельзя, т. к. 
, и уравнение (51.13) принимает вид
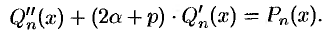
В левой части — многочлен степени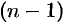 
, в правой части — многочлен степени . Чтобы получить тождество многочленов в решении 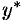, нужно иметь многочлен степени 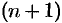. Поэтому частное решение 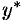следует искать в виде 
(в равенстве (51.12) положить 
).
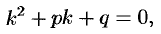в) Пусть является двукратным корнем характеристического уравнения , т. е. 
. В этом случае и 
, а поэтому уравнение (51.13) принимает вид 
.
Слева стоит многочлен степени 
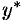. Понятно, чтобы иметь слева многочлен степени , частное решение следует искать в виде
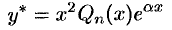
(в равенстве (51.12) положить 
).
Случай 2. Правая часть (51.10) имеет вид
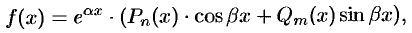
где 
и 
— многочлены степени и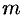 
соответственно, 
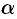и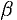 
— действительные числа. Уравнение (51.10) запишется в виде
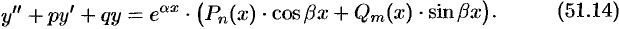
Можно показать, что в этом случае частное решение 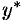уравнения (51.14) следует искать в виде
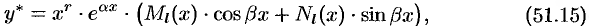
где 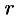— число, равное кратности 
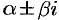как корня характеристического уравнения , 
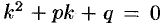и 
— многочлены степени 
с неопределенными коэффициентами, — наивысшая степень многочленов и , т. е. 
.
Замечания.
- После подстановки функции (51.15) в (51.14) приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения.
- Форма (51.15) сохраняется и в случаях, когда
или 
. - Если правая часть уравнения (51.10) есть.сумма функций вида I или II, то для нахождения 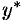следует использовать теорему 51.2 о наложении решений.
Пример №51.2.
Найти общее решение уравнения 
.
Решение:
Найдем общее решение 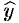ЛОДУ 
. Характеристическое уравнение 
имеет корень 
кратности 2. Значит, 
. Находим частное решение исходного уравнения. В нем правая часть 
есть формула вида 
, причем 
, не является корнем характеристического уравнения: 
. Поэтому, согласно формуле (51.12), частное решение 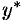ищем в виде 
, т. е. 
, где 
и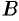 
— неопределенные коэффициенты. Тогда 
. Подставив ,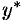 
, 
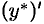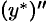в исходное уравнение, получим 
, или 
. Приравнивая коэффициенты при одинаковых степенях , получаем систему уравнений:
Отсюда 
. Поэтому частное решение данного уравнения имеет вид 
. Следовательно, 
— искомое общее решение уравнения.
Дополнительный пример №51.3.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
