Оглавление:

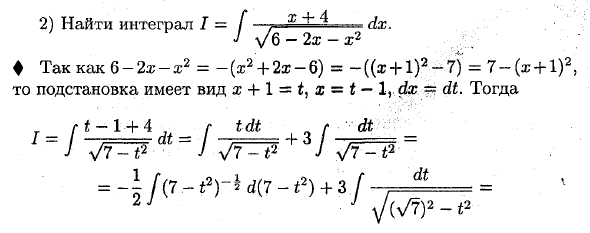



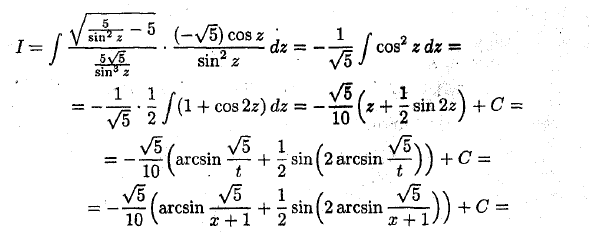



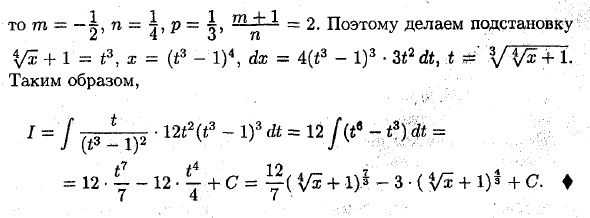
Интегрирование иррациональных функций
- Иррациональная интеграция функция wjr ‘ Давайте рассмотрим несколько типов интегралов, включая иррациональные функции. в Тип интеграции [> ■■, [y / ax2 + bx 4- cdx \ ■ ..; ..- ^ vax2 4- bx 4- s ^ m-mrc + fr ^ pjx можно найти как: iod pa- » l / ax2 4- bx 4- s В дикой природе, выберите полный квадрат Ax2 4-BX 4-C = Затем сделайте замену x 4- ^ = t.
Пример: 1) интеграл / = [, J V 4×2 4-2z + 1 ♦ 4×2 4- 2x + 1 = i (если x2 4- ^ x 4- = 4-4- дх 1 г дх L r dx _ 1 г ~~ J l, /, ig gt; «2 J > / * ((* + M> 2 + &> 27 + *) * + £ ‘ Сделайте замену; 4- ^ = = = — ^, dx = dt. тогда и + с. ♦ dt 1, = -In v «2 + 3/16 2 x + \ + Axe + \ Y + Tb Тогда m = — ~, n = ~ m £ 1 = 2. Таким образом, U + 1 = i3, X = (t8-l) 4, dx = 4 (£ 3-l) 3. 3 * 2 дт, т V V ^ +1. Таким образом, 1 = I (1z ~ [) 2 ‘^ ~ D3 dt = l2f («• -t?) * = = 12 y-12 • j + C = y (Vi + 1) 1-3 • (V® + 1) ‘1 + C.
В этом случае первые два интеграла являются табличными, а третий интеграл является суммой двух табличных интегралов. Людмила Фирмаль
2) Найти интеграл I = [j x + ^ dx. J V6-2x-x2 4 6-2x-x2 = ~ {x2 + 2x-G) = — ((z + 1) 2-7) = 7- (x + 1) 2, поэтому формат перестановки равен a. + 1 = t, x = t-lydx-dt. тогда rt-1 + 4, g tdt „f” dt = -lf (7-f>) -ld (7-t *) + 3 [dt = 1 J J y (\ / 7) 2-t2= — \ / 7-t2 -t-3-arcsin 4 = + = 3 arcsin-l / b-2x-x2 + C. ♦ V7 V 7 II. Ямтеврали «….. Где a, 6, c, d — действительные числа, a, p, …, (5, 7 — натуральные числа, Броненосец фракция q, …, £.
От замены j? = £ fc следует £ = C «E» t d .Jkrft * J — dhtk ~ 1 [ctk-a) — (b-dtfc) cfetfe «» 1 ^ ■, fc.wT и — * — J. «Большой (доктор) Родился из разумной функции т. Также каждый Степень дроби выражается рациональной функцией от t. Пример: 1) Интеграл I = [~ -, ‘J Y (x + 2) 2-jx + 2 ♦ Наименьшее общее кратное знаменателя | и ^ являются б. Поэтому введите x + 2 = a: = -2, tfo = 6t5 dt% t = +2. Таким образом, = 6Д <+ 1 4- ^ j-) dt = З * 2 + б <+ бIn | t-1 | + c = = 3. Vx + 2+ V5T2 + 61n | V5T2-1I + s. ♦ 2) Указывает на подстановку, чтобы найти интеграл. g-f 1 ^ g _ f s p 4-1 dx
Для Ii перестановка x = t2, для 2 перестановка x ‘: = £ 3. ♦ III. Введите j Integr (x; \ / a’2-x2) dxf R (x \ \ / a2 + x2) dx-интеграл, ; x2-a2) dx сводится к интегралу функции, которая разумно зависит от тригонометрической функции, используя следующую перестановку тригонометрических функций. x = a ■ sin t, первая интеграция. x = a • tg второго интеграла. х = -3-й интеграл./ г / л X2 Y ^ -dx. «» ♦ Положить x = 2 sin t} dx = 2 cos tdt> t = arcsin ^. тогда дт = r v4-4sin £. 7J / -4cos2t Я = — ^ — 2costdt = / — J 4 син т J 4 син т = fl- ^ ldt = fJ * -fdt ‘= — * gt-t + c = J sin £ J sin t J г / 4-х2 „. X /. X \, x -C-arcsin — ctg (arcsin-) = C-arcein — 2 \ 2/2 Вт V * грех * §I ‘
| Основные методы интегрирования | «Берущиеся» и «Неберущиеся» интегралы |
| Интегрирование тригонометрических функций | Определенный интеграл как предел интегральной суммы |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Внутривенно Интеграция типа JR (x) y / ax2 + bx + c) dx. Это интеграл Функция aral является рациональной функцией для x и y / ax2 + bx + c. Если вы выберете идеальный квадрат под радикалом и выполните перестановку x + t = t}, показанный тип интеграции (IV) будет уже рассмотренным типом интеграции, то есть интегрированием. Тип f R (t; yja2-t2) dt} f R (t; y / a2 + t2) dt, f R (t \ Vt2-a2) dt. Эти интегралы могут быть вычислены с использованием соответствующих тригонометрических перестановок. _ / \ / x2 -f- 2x ~ 4 ♦ r2 + 2a; -4 = (x + I) 2-5, x + 1 = t, x = t-1, dx-dt. Следовательно, I = f Vfo-5 dt. i = dt = «Vb-cosz dz, J J t6 sin g ‘sin2z r = arcsin Тогда
V 0 (- \ / 5) cosz, If®J —7 = —— dz = —p / cos1 zdz = грех зб / ш- / грех1 * г = —L. 11 (1 + cos 2 *) = (x + | sin 2 *) 4-С ^ arcsin — + — sm ^ 2 arcsin-J J + С = + C = 10 г / б (л / 5 1./l. л / 5 \ arcsin— + -sm 2 arcsin— V ar + l 2 V x + lJJ у / б /. y / b, y / e-y / x2 + 2x ~ 4 \ t ^ , = — (Arcsm-4-: ——-) +. С. ♦ 10 В: x + 1./(x 4-1) 2 / • Примечания: интеграл типа f \, предпочтительно J x y ax2 4- bx 4- s Ходить с джокером = «C V. интеграл типа -dx, Pn (x) — многочлен В ^ V ах2 4- 4- с
^ L / o. … х г J y / ax1 4-oh 4-s ‘>> л. ;. : 1 * u Qn-i (x) — это многочлен порядка n-1 неопределенного коэффициента, а A также является неопределенным коэффициентом. Все неопределенные коэффициенты выводятся из тождества, полученного путем дифференцирования обеих сторон уравнения (1). , F’fy = (Qn-iM • Vax * + bx + c) ‘+ *, y / ax1 4-bx 4-s 4-bx 4-s Тогда нам нужно выровнять коэффициенты с тем же порядком неизвестного х. Пример: интеграция / = / x = da; Найдите. ♦ Согласно формуле (1): , 2 / = [. X-d dx = (Lx + B) y / 1-2x-x2 + [- \ / 1-2x ~ x2 Y J / 1-2x- x2
Вы можете рассчитать pj, используя следующее уравнение: h / ax2 + bx 4-s (1) Я Людмила Фирмаль
Различение этого равенства дает:y / l-2x-x2 2Vl-2x-x2 Vl-2x ~ x2 Это x2 == A (1-2x-x2) -f (Ax + B) (-1-x) + A, x2 = A — Ac2-Ax- B-Ax2-Bx + L. Сравните коэффициенты с той же степенью х. {1 = -A-x’2 A Х = O = -2A до A-B, x = O = A-B + A.
Следовательно, A = -r Aj B = A = 2. Таким образом, f-; A 3 \ r ——. Д д дх y / 2- [x + I) ‘2 f, = («c + |) y / 1-2x-x * 4-2arcsin + C • «In. G • тип интегрирования / xm ‘(a + bxn) p dx (называемый дифференциальной биномиальной интеграцией), где a, 6 — действительные числа. Пπη> ρ — рациональное число, P.A. Как показывает Чебышев, рассмотрим случай, когда хотя бы одно из чисел p, ^^ или + 1 4-p является целым числом.
Рационализация интеграла в этих случаях осуществляется следующей подстановкой: 1) Перестановка x = tk, если p целое число. Где k — наименьшее общее кратное знаменателей дробей m и n. 2) Если 171 <r является целым числом, заменить 4-bxn = где Техас s знаменатель дроби p \ 3) Когда 2L ± -1 + p является целым числом, заменить 4-bxn-xn t *, н * Где s — знаменатель дроби p. Во всех остальных случаях интеграл типа xm (a 4-bxn) p dx Он не выражается известной элементарной функцией, то есть его нельзя взять. Пример: Найти интеграл 1 = 1 v ‘^ dx. ♦ и позже

