Оглавление:
Интегрирование функции комплексного переменного
Определение, свойства и правила вычисления интеграла
Пусть в каждой точке некоторой гладкой кривой 
с началом в точке 
и концом в точке 
определена непрерывная функция 
.
Разобьем кривую на 
частей (элементарных дуг) в направлении от к 
точками 
(см. рис. 287).
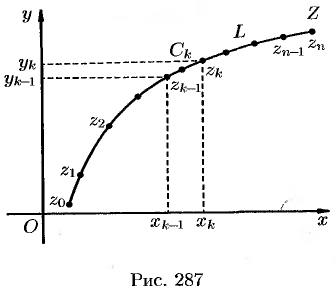
В каждой «элементарной дуге» 
выберем произвольную точку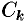 
и составим интегральную сумму 
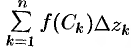, где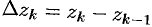 
.
Предел такой интегральной суммы при стремлении к нулю длины наибольшей из элементарных дуг, если он существует, называется интегралом от функции по кривой (по контуру) и обозначается символом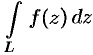 
.
Таким образом,
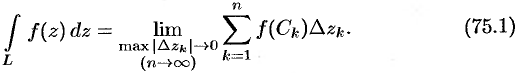
Покажем, что если — гладкая кривая, a — непрерывная и однозначная функция, то интеграл (75.1) существует.
Действительно, пусть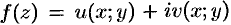 
, 
, 
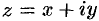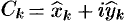. Тогда
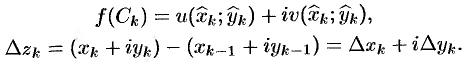
Поэтому
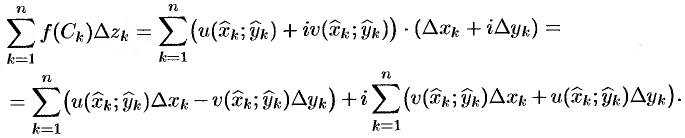
Обе суммы, находящиеся в правой части последнего равенства, являются интегральными суммами для соответствующих криволинейных интегралов (см. п. 56.1).
При сделанных предположениях о кривой и функции пределы этих сумм существуют. Поэтому после перехода к пределу (в последнем равенстве) при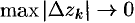 
получим:
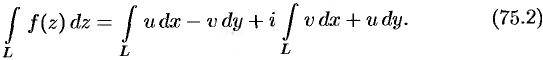
Формула (75.2) показывает, что вычисление интеграла от функции комплексного переменного сводится к вычислению криволинейных интегралов от действительных функций действительных переменных.
Формулу (75.2) можно записать в удобном для запоминания виде:
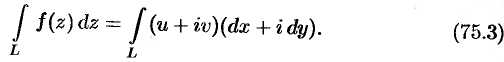
Если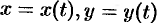 
, где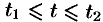 
— параметрические уравнения кривой , то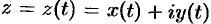 
называют комплексным параметрическим уравнением кривой ; формула (75.3) преобразуется в формулу
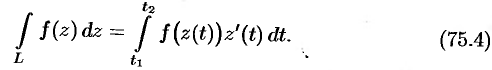
Действительно, считая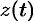 
непрерывной и дифференцируемой функцией, получаем
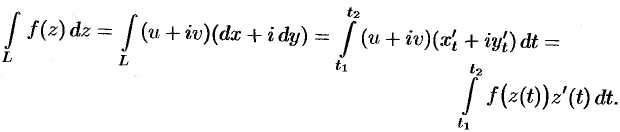
Приведем основные свойства интеграла от функции комплексного переменного.
.
, 
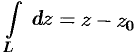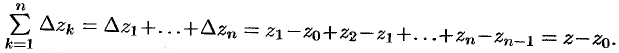
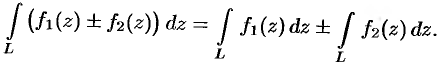
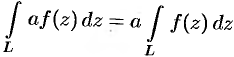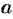— комплексное число.
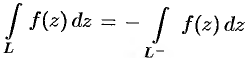, т. e. при перемене направления пути интегрирования интеграл изменяет свой знак на противоположный (в других обозначениях кривой: 
).
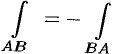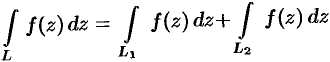, где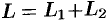 
, т. e. интеграл по всему пути равен сумме интегралов по его частям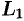 
и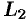 
.- Оценка модуля интеграла. Если
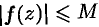во всех точках кривой , то 
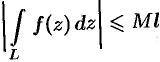, где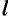 
— длина кривой .
Действительно,
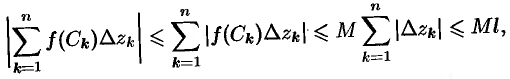
где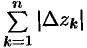 
— длина ломаной 
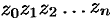, вписанной в кривую .
Все приведенные свойства интеграла функции комплексного переменного непосредственно вытекают из его определения (75.1) и представления (75.2).
Пример №75.1.
Вычислить
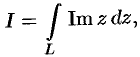
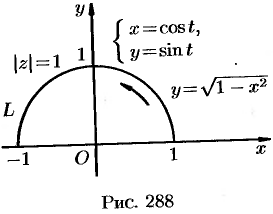
где — полуокружность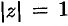 
, 
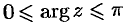(см. рис. 288).
Решение:
Используя формулу (75.3), имеем:
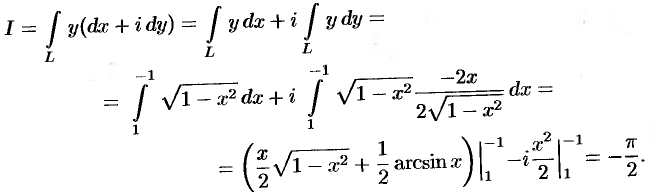
Используя формулу (75.4), имеем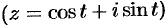 
:
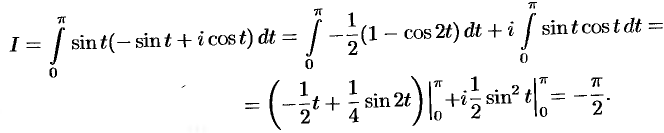
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Аналитическая функция тфкп |
| Геометрический смысл модуля и аргумента производной |
| Интегральная теорема Коши |
| Интеграл Коши. Интегральная формула Коши |
