Оглавление:
Интегрирование дифференциальных уравнений движения материальной точки в простейших случаях
Ко второй основной задаче динамики точки относятся те задачи. в которых известны силы, действующие на материальную точку, и требуется определить закон ее движения. Пели точка несвободна. то в правую часть уравнений войдут также неизвестные реакций связей, и потому вторая задача динамики в этом случае, состоит в том, чтобы, зная действующие на точку активные силы, определить ее движение и реакции наложенных на нее связей.
Вторая задача решается интегрированном дифференциальных уравнений (111) движения материальной точки в декартовых координатах или естественных уравнений (112) ос движения.
Значения постоянных интегрирования, появляющихся в процессе интегрирования дифференциальных уравнений, находятся для каждой частной задачи из так называемых начальных условий, определяющих положение и скорость точки для какого-либо определенного момента времени.
При решении второй задачи динамики точки полезно придерживаться следующей последовательности:
- Выбрать систему координат. Начало декартовых координат нередко бывает удобно совмещать с начальным положением точки. Оси же координат удобно направлять так, чтобы координаты точки и проекции ее скорости на координатной от в рассматриваемый момент времени были положительными. Если точка движется по прямой, то эту прямую принимают за ось. Пели траектория движения точки известна, то удобно пользоваться осями координат. За начало координат в этой системе принимается положение точки и произвольный текущий момент.
- Изобразить положение движущейся материальной точки в произвольный текущий момент времени и показать на рисунке все действующие на точку силы, в том числе, обязательно и реакции наложенных на 1 ч-е связей.
- Записать начальные условия движения точки.
- Спроектировать на выбранные координатные оси псе силы, действующие на точку, и подставить алгебраические суммы проекций всех сп.т на соответствующие оси в правые части уравнений (111) или (112). При этом переменные силы, действующие па точку, надо обязательно выразить через те величины, от которых они зависят.
- Проинтегрировать полученные дифференциальные уравнения методами, известными из курса высшей матч матикн.
- Использовав начальные условия движения точки, определить постоянные интегрирования. Постоянные интегрирования часто целесообразно определять непосредовепно после каждого интегрирования. В некоторых случаях, вместо введения постоянных интегрирования, оказывается более удобным брать от обеих частей равенства определенные интегралы в соответствующих пределах.
- Установив закон движения материальной точки, определить искомые в задаче величины.
Процесс интегрирования дифференциальных уравнений движения показан ниже i:a примерах решения четырех задач. Первая из них — на криволинейное движение свободной материальной точки под действием постоянной силы. Следующие две — па прямолинейное движение точки под действием переменной силы, когда она является либо только функцией времени, либо только функцией скорости; четвертая задача относится к случаю криволинейного движения несвободной точки по заданной траектории. Примерами решения второй задачи динамики являются и случаи, рассмотренные в следующей главе.
Пример задачи:
Материальная тонка 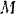 брошена под углом
брошена под углом 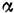 к горизонту с начальной скоростью
к горизонту с начальной скоростью 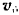 . Пренебрегая сопротивлением воздуха, определить: 1) уравнения движения точки
. Пренебрегая сопротивлением воздуха, определить: 1) уравнения движения точки
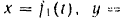
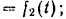
2) траекторию движении точки; 3) дальность 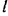 полета точки при данном угле
полета точки при данном угле 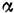 и 4) уют
и 4) уют 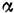 при котором дальность полета точки будет наибольшей.
при котором дальность полета точки будет наибольшей.
Решение:
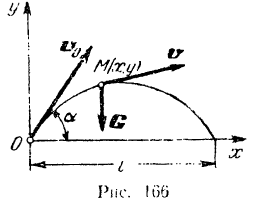
Примем начальное положите 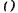 точки за начало координат и проведем горизонтальную ось v и вертикальную так, чтобы начальная скорость
точки за начало координат и проведем горизонтальную ось v и вертикальную так, чтобы начальная скорость 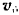 точки лежала в плоскости
точки лежала в плоскости 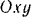 (рис. 166;. При таком выборе координатных осей точка будет совершать движение в плоскости
(рис. 166;. При таком выборе координатных осей точка будет совершать движение в плоскости 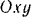 . так как на нее действует только сила тяжести
. так как на нее действует только сила тяжести 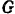 , расположенная в той же плоскости. Изобразим данную точку в произвольном положении
, расположенная в той же плоскости. Изобразим данную точку в произвольном положении 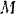 .
.
Проекции силы, действующей на точку,
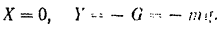
Подставляя эти значения и дифференциальные уравнения движения точки, будем иметь:
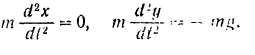
Сокращая обе части каждого из уравнений на массу точки, получим:
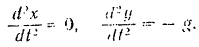
Решаем сначала первое из данных уравнений:
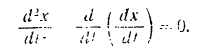
Интегрируя его, находим:
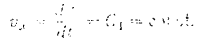
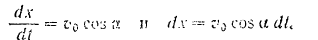
Интегрируя последнее уравнение, находим
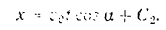
Значение произвольной постоянной 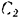 вдоль находим из начальных условии: при
вдоль находим из начальных условии: при
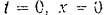
Подставляя эти значения 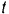 и
и 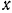 в предыдущее равенство, получаем
в предыдущее равенство, получаем
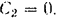
Следовательно, решенном парного из данных дифференциальных уравнений будет
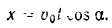
Переходим к решению второго дифференциального уравнения:
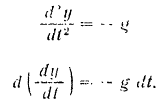
Интегрируя это уравнение, получим:
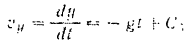
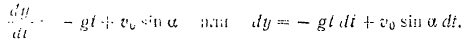
Интегрируя последнее уравнение, получаем:
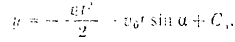
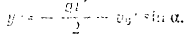
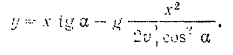
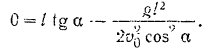
Решая это уравнение относительно 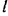 , получим:
, получим:
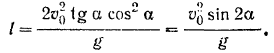
Так как наибольшее значение
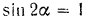
при
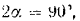
то из последней формулы следует, что наибольшая дальность
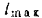
по а точки (при данной величине ее начальной скорости 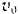 ) всегда соответствует углу бросания
) всегда соответствует углу бросания
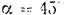
Нужно, конечно, иметь в виду, что этот вывод Пак же как и уравнения движения точки по тучен нами без учета влияния сопротивления воздуха ни движение точки, т. е. справедлив лишь при ее движении в пустоте.
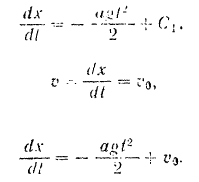
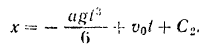
Для того чтобы определить тормозной путь 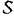 , из уравнения (I) находим время торможения
, из уравнения (I) находим время торможения 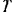 , полагая скорость в конце пути
, полагая скорость в конце пути 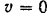 :
:
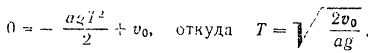
Подставляя значение 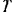 и
и 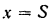 в уравнение (II), находим:
в уравнение (II), находим:
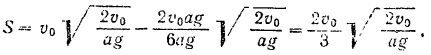
Пример задачи:
Тело надает без начальной скорости с небольшой, по сравнению с радиусом Земли, высоты. Сила сопротивления воздуха
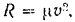
где 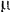 — коэффициент сопротивления. Найти зависимость скорости тела от времени падения, а также предельную скорость тела. Вследствие небольшой высоты падения силу тяжести
— коэффициент сопротивления. Найти зависимость скорости тела от времени падения, а также предельную скорость тела. Вследствие небольшой высоты падения силу тяжести 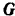 тела и коэффициент сопротивления
тела и коэффициент сопротивления 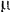 можно считать постоянными.
можно считать постоянными.
Решение:
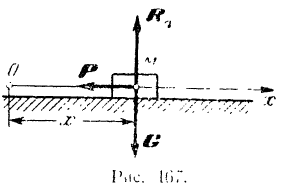
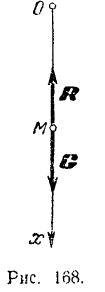
Так как при падении тело будет двигаться поступательно, то его можно рассматривать как материальную точку. За начало 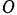 координат примем начальное положение этой точки. Ось
координат примем начальное положение этой точки. Ось 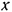 направим вертикальную вниз. На точку
направим вертикальную вниз. На точку 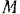 действуют силы:
действуют силы: 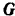 — сила тяжести тела и
— сила тяжести тела и 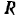 — сила сопротивления воздуха, направленная в сторону, противоположную движению тела (рис. 168). Проекция этих сил на ось
— сила сопротивления воздуха, направленная в сторону, противоположную движению тела (рис. 168). Проекция этих сил на ось 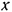 :
:
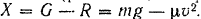
Дифференциальное уравнение движения точки 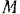 будет иметь вид
будет иметь вид
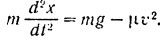
В случае прямолинейного движения точки по оси 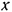 :
:
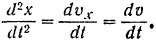
Подставляя это значение в предыдущее уравнение и сокращая обе части его на 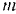 , будем иметь:
, будем иметь:
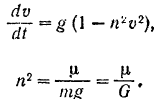
Как видно из уравнения (I), при наличии сопротивления среды, движение падающего тела не будет равноускоренным (как в пустоте). Тело сначала быстро увеличивает свою скорость, а затем, по мере увеличения сопротивления, его движение приближается к равномерному с некоторой предельной скоростью 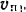 .
.
Из уравнения (I) находим, что при
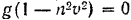
ускорение падающего тела
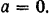
Отсюда его предельная скорость
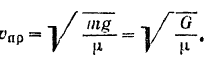
Предельная скорость зависит, следовательно, от веса тела и коэффициента 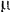 сопротивления среды.
сопротивления среды.
Для того чтобы найти зависимость скорости падающего тела от времени, разделим переменные в уравнении (I):
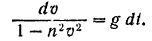
Выражение, стоящее в левой части последнего уравнения, можно представить в виде
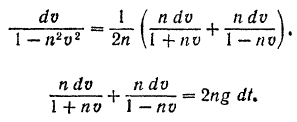
Интегрируя это равенство, получим:
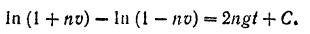
Согласно начальным условиям: при
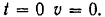
Подставляя эти значения в предыдущее уравнение, находим значение постоянной интегрирования:
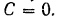
Таким образом,
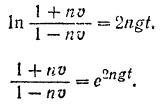
Решая это уравнение относительно 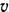 , найдем:
, найдем:
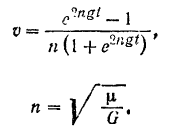
Пользуясь данной зависимостью, можно определить скорость падающего в воздухе тела а любой момент времени. Если разделить числитель и знаменатель правой части равенства (II) на 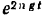 , то мы получим:
, то мы получим:
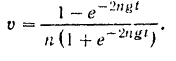
При достаточно большом коэффициенте сопротивления
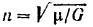
дробь
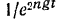
быстро приближается к нулю, а скорость падающего тела — к значению
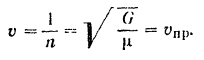
Пример задачи:
На горизонтальной плоскости лежит точка 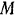 , привязанная нитью длиной
, привязанная нитью длиной 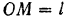 к неподвижной точке
к неподвижной точке 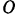 плоскости. Точке
плоскости. Точке 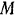 сообщена начальная скорость
сообщена начальная скорость 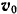 . перпендикулярная к направлению натянутой нити, вследствие чего точка
. перпендикулярная к направлению натянутой нити, вследствие чего точка 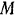 описывает на плоскости окружность. Найти зависимости от времени скорости точки и силы натяжения миги, если известны все
описывает на плоскости окружность. Найти зависимости от времени скорости точки и силы натяжения миги, если известны все 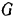 точки и коэффициент
точки и коэффициент 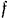 трения.
трения.
Решение:
Траектория движения несвободной материальной точки  нам известна. Удобно воспользоваться в этом случае естественными уравнениями движения точки. За начало естественных осей координат возьмем произвольное положение точки
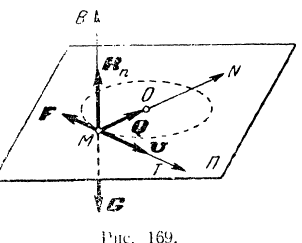
нам известна. Удобно воспользоваться в этом случае естественными уравнениями движения точки. За начало естественных осей координат возьмем произвольное положение точки  на окружности и направим оси так как показано на рис. 169.
на окружности и направим оси так как показано на рис. 169.
К точке  приложены силы: сила
приложены силы: сила 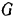 тяжести, направленная по бинормали
тяжести, направленная по бинормали 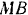 вертикально вниз, нормальная реакция
вертикально вниз, нормальная реакция 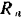 плоскости, направленная по бинормали вертикально вверх, сила
плоскости, направленная по бинормали вертикально вверх, сила 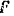 трения, направленная по касательной
трения, направленная по касательной 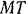 в сторону, противоположную вектору
в сторону, противоположную вектору 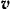 скорости точки и реакции
скорости точки и реакции 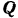 нити, направленной по главной нормали
нити, направленной по главной нормали 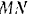 к центру
к центру 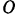 окружности. Начальное условие: при
окружности. Начальное условие: при
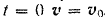
Проектируя все силы, приложенные к точке 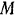 , на оси естественных координат, будем иметь:
, на оси естественных координат, будем иметь:
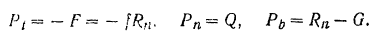
Естественные уравнения (112) движения точки в нашем случае принимают вид
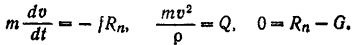
Из последнего уравнения находим
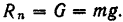
Подставляя это значение 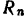 в первое из уравнений, будем иметь
в первое из уравнений, будем иметь
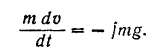
Разделяя переменные в этом уравнении и интегрируя его в соответствующих пределах, находим:
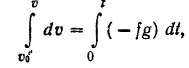
откуда
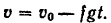
Принимая во внимание, что радиус 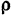 кривизны траектории (окружности) равен длине
кривизны траектории (окружности) равен длине 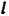 нити, из второго уравнения системы находим реакцию нити (равную по модулю силе ее натяжения)
нити, из второго уравнения системы находим реакцию нити (равную по модулю силе ее натяжения)
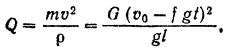
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

