Оглавление:
Интегрирование дифференциального бинома
Интегралы типа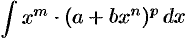 
(называемые интегралами от дифференциального бинома), где 
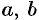— действительные числа;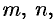 
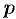— рациональные числа, берутся, как показал Чебышев П.А., лишь в случае, когда хотя бы одно из чисел 
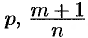или 
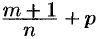является целым.
Рационализация интеграла в этих случаях осуществляется следующими подстановками:
1) если 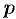— целое число, то подстановка 
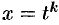, где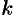 
— наименьшее общее кратное знаменателей дробе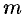й 
и 
;
2) если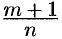 
— целое число, то подстановка 
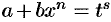, где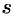 
— знаменатель дроби ;
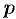3) если 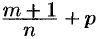— целое число, то подстановка 
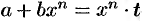, где 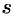— знаменатель дроби .
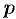Во всех остальных случаях интегралы типа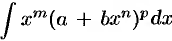 
не выражаются через известные элементарные функции, т. е. «не берутся».
Пример №33.8.
Найти интеграл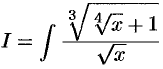 
.
Решение:
Так как
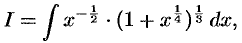
то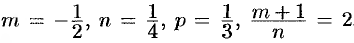 
. Поэтому делаем подстановку 
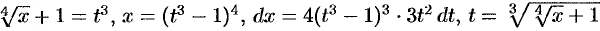. Таким образом,
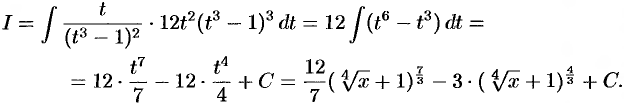
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Тригонометрическая подстановка |
| Интегралы типа r x (ax^2+bx+c) dx |
| «Берущиеся» и «Неберущиеся» интегралы |
| Определенный интеграл как предел интегральной суммы |
