Оглавление:





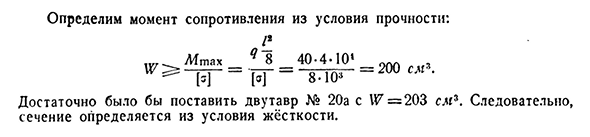

Интегрирование дифференциального уравнения изогнутой оси балки при двух участках.
- Интеграл дифференциальных уравнений криволинейной оси балки на двух участках. Если изгибающий момент в разных частях балки представлен разными формулами, то необходимо составить такое же количество дифференциальных уравнений, как и площадь на балке. Нагружают силой р на расстоянии от левой балки на двух опорах
в пролете Z, b от правой кромки b; пусть a » >B(рис. 287). Поддерживающий отклик луча равен H A=0, B=^ -. Возьмите начало координат левой опоры и правую ось X. Изгибающий момент в первом и втором сечениях выражается различными уравнениями^поэтому мы можем найти два произвольных сечения в абсциссах x^и x%. Значения y, M, C, D и абсциссы раздела
уравнения отмечены в индексе 1 первого раздела и индексе 2 второго. При Людмила Фирмаль
составлении моментального представления обеих секций рассмотрим левую часть балки, а затем первую секцию: l R Ml=LX1=Y Xi, для второй секции (секция O2): R М=А% — Р(х2-а)= — х — р(х2-а). Интегрирование термов вида P (x2-a) осуществляется без скобок, как это сделано в Примере 74. При этих условиях вычисление выглядит следующим образом: П Е Р В ы й Г А С Т О К Т О Р У ч а с Т О К А Д=M1=Dx1; EJy= — (18.31) Ежи’и=L42=DH2-Р(х2-а); ежи и=-Р(х2-а); с т Pbxl +(18.33) 4-C2×2 4-D2. (18.34) выражение для отклонения и вращения включает Интеграл четырех констант. Чтобы определить эти константы, нужно
написать четыре уравнения. Эти уравнения, как и в предыдущем случае, что-то знают о прогибе и угле поворота, всегда можно сделать, рассматривая сечение пучка таким сечением вещества является: Участок с, расположенный на границе двух участков, можно отнести как к первому, так и ко второму из них. Итак, величину прогиба и угла поворота сечения С можно вычислить как по формуле первого сечения, так и по формуле второго: то есть x1=x2=a; Если значение получено и B1=9a или y и 0, то оно должно быть одинаковым. Ежи=Ежи Альф () е дя^^е дя^. (b)§ 112]уравнение
- криволинейной оси балки в двух сечениях 363 Таким образом, точки деления графика всегда дают два уравнения. Сечение A при x t=0 отклонение YG=O, ©> «B«x=I>y2=0. Подставляя выражения (18.31) и (18.33) вместо X}и уравнивая значение и правильную часть X% a, получаем условие (a): P A2|p_ _ R a * g>(A~°) 8 I2-I2P2 Откуда (18.35)) Аналогично она получается по условиям из формул (18.32) и (18.34 (&): 7• + ЦРУ+°я=7^ — П(°Б-«Б» Б Д Откуда Di=D(18.36) следовательно, константы интегрирования для обоих участков были одинаковыми. Это связано с принятием метода композиции и интегрирования
дифференциальных уравнений. Когда Формула (18.32) применяется к эталонному участку D, она получается на основе © Oh=09, следовательно, O9=0. Применение той же формулы (18.34) к ссылочному разделу B дает результаты, основанные на (d Здесь уравнения для y и 6 принимают следующий вид: 364 аналитические методы определения деформации[глава XV. Рассмотрим значение максимального прогиба f. это будет сечение с 0=0. Из формулы для 0! Мы видим это для X1=0., РА’ЗЕЛ площадь поперечного сечения В=а (И — #); Так как B<^a, то значение 01^>O. Таким образом, 0t
между точкой А и точкой с меняет знак, то есть проходит через ноль. Людмила Фирмаль
Значит, наибольший прогиб будет у первого участка. Чтобы найти абсциссу xj соответствующего сечения, подставим это значение xj в выражение 0A и сделаем его равным нулю: — -^ -(/2 — £2) | = 0; таким образом, xj=1 — • Поэтому при перемещении от середины пролета к опоре Фигура. Центральный прогиб пролета 287 Два. В этом легко убедиться, подсчитав небольшую разницу между Если вы присваиваете выражению Y lf, RZ (R-B) / z (R-B*)RRU’Z l / ~((18 37) 27EJZ-21EJ V\Z2/’ Расстояние участка с наибольшим отклонением
от левой опоры изменяется с изменением положения груза. Если сила P находится в середине пролета、 /. £Р/5 −2’Max-4 8£/, (18.38) Если переместить силу P на правую опору и установить предельное расстояние b равным нулю, то#->0; x0=—=x= = 0,577/. Tplt/ Из точек D и B (рис. 288) абсцисса точки с наибольшим отклонением изменяется только между 0,5/и 0,577 / между точками D и R. особенно при размещении Фигура. 288. (18.39) Число /Ш В Я/^.§ 1 1 2] формула для криволинейной оси балки на двух участках 3 6 5 П р и М Е Р 77.
Подобрать сечение стальной двутавровой балки с непрерывной нагрузкой q=4 т/м на полпролета(рис. 289), если пусковое напряжение[а]=1000кг/см2, а допустимое отклонение не должно превышать-jOOQ-пролет равен/=2,0 м. Давайте положим начало координат в точке I, ось x находится справа, а ось y-вверху. Нумерация участков показана на рисунке. Мы составляем и интегрируем дифференциальные уравнения криволинейных осей, считая
x на обоих участках от точки A. fl- Два. Фигура. Двести восемьдесят девять ЭДЖ ЭДЖ d2y * ДХ% Т О Р О й=м2, у ч а с т о с д Х2″2\2 2)’ EJys— — ^4″ —— 2^} ^2* Один. Два. Интегральная константа определяется из условия: x3= / » x » должно быть 2 = / >» ^8 = 0. х t=хз я Два» >> акстись Д х s’ >X i=X s I −2 >Эжит=Эжит. Дайте первые два условия: с 2_|?/ 8р-7?/ 4-7?/ 4 * ■48 ′ 16-24-384 * Из третьего и четвертого условий: Ди = ДС = 7?/ 4 Триста восемьдесят четыре Запишите уравнение прогиба первой секции в последней форме, так как максимальное прогибание будет иметь конец балки. Y ’~[+48 ′ 384J-384EJ L8I+G Максимальное отклонение (x=0)/= — Iql * WAEJ * Теперь мы можем
определить J: / _ из жестких условий. 7^ — 3 8 4£7′ Iql 7.40-8- 10E-103 384.2-10° 7= = 2910см. I балка № 24 момент инерции 7=3460см\366 метод анализа для определения деформации[гл. XVIII Определите момент сопротивления из условий интенсивности: Afmax8″ — — — Т Т-8-10″ — * * * см>’ I луч No. It достаточно разместить 20A С W=203cm*. Таким образом, поперечное сечение определяется из условий жесткости.
Смотрите также:

