Оглавление:
Некоторыми сложными функциями будем считать функции вида 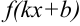 , где
, где 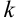 и
и 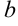 — любые действительные числа. Так,
— любые действительные числа. Так, 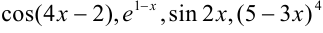 — примеры некоторых сложных функций. В аргументе этих функций переменная
— примеры некоторых сложных функций. В аргументе этих функций переменная  находится только в первой степени!
находится только в первой степени!
Для нахождения интеграла от некоторых сложных функций будем использовать формулу: 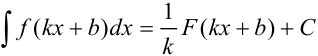 . Ее правильность легко проверяется дифференцированием обеих частей.
. Ее правильность легко проверяется дифференцированием обеих частей.
Можно также применять следующий алгоритм:
- Выбрать табличный интеграл, к которому сведется данный.
- Вместо
 в табличном интеграле подставить выражение
в табличном интеграле подставить выражение 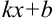 из исходного интеграла.
из исходного интеграла. - В правую часть добавить множитель
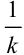 , где
, где 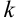 — коэффициент перед
— коэффициент перед  .
.
Рассмотрим нахождение интеграла от некоторых сложных функций на примерах.
Пример №19.4.
Найдите 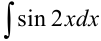 .
.
Решение:
Видим, что под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 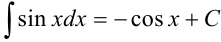 .
.
В нашем примере в качестве аргумента выступает угол 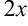 . Выделим коэффициент
. Выделим коэффициент 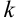 , стоящий перед
, стоящий перед  :
: 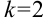 , следовательно, в правую часть мы должны добавить множитель
, следовательно, в правую часть мы должны добавить множитель 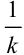 , то есть
, то есть 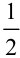 . Тогда получим, что
. Тогда получим, что 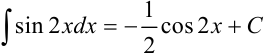 .
.
Пример №19.5.
Найдите 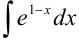 .
.
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 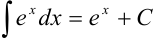 .
.
В примере в качестве аргумента выступает выражение 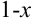 . Выделим коэффициент
. Выделим коэффициент 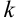 , стоящий перед
, стоящий перед  :
: 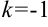 , следовательно, в правую часть добавим множитель (-1). Тогда получим, что
, следовательно, в правую часть добавим множитель (-1). Тогда получим, что 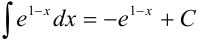 .
.
Пример №19.6.
Найдите 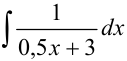 .
.
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 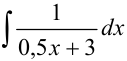 .
.
В примере в качестве аргумента выступает выражение 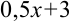 . Выделим коэффициент
. Выделим коэффициент 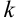 , стоящий перед
, стоящий перед  :
: 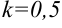 , следовательно, в правую часть добавим множитель 1:0,5=2. Тогда получим, что
, следовательно, в правую часть добавим множитель 1:0,5=2. Тогда получим, что 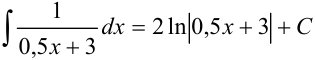 .
.
Пример №19.7.
Найдите 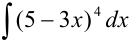 .
.
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 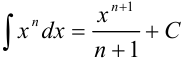 .
.
В примере в качестве аргумента выступает выражение 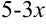 . Выделим коэффициент
. Выделим коэффициент 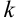 , стоящий перед
, стоящий перед  :
: 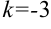 , следовательно, в правую часть добавим множитель (-1/3). Тогда получим, что
, следовательно, в правую часть добавим множитель (-1/3). Тогда получим, что 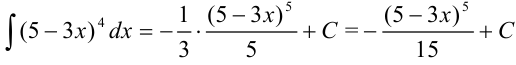 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Таблица основных интегралов. |
| Непосредственное интегрирование. |
| Интегрирование методом замены переменной (методом подстановки). |
| Метод интегрирования по частям. |

