Оглавление:




Интегральный признак сходимости рядов с неотрицательными членами
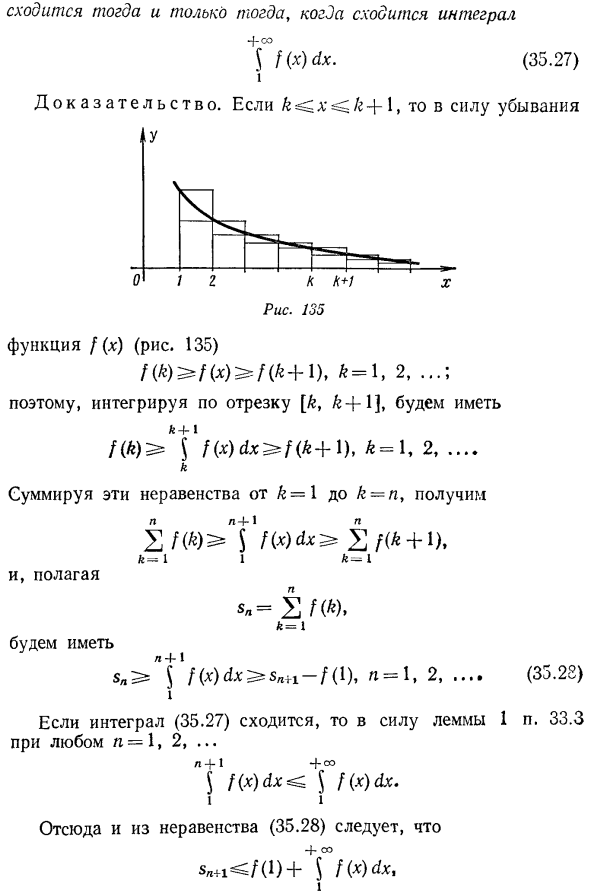
Интегральный признак сходимости рядов с неотрицательными членами. Если для заданного ряда (35.1) можно выбрать функцию, определенную в x^\, например/(α)=»», то при определенных условиях можно выбрать функцию из сходимости или расходимости интегралов. $ / (х) DX Вы также можете определить сходимость или расходимость ряда(35.1). Теорема 10 (интегральный критерий сходимости рядов).Если функция f (x), определенная для всех x> 1, не отрицательна, а убывает, то ряд И (35.26) 2 /(я) § 35.Числовой ряд 562. Сходятся только тогда, когда Интеграл сходится 4-х | !{х) ых. (35.27) Доказательство. если k ^ x ^ k + 1, то по убывающей Функция I (x) (рис. 135) НК)^ НК)^ УП + 1), к = 1, 2,…;Следовательно, если мы интегрируем в интервале μ, г+ 1]、 64-1 Hk)^ $Цχ) х^^ -^ -), k=\, 2 Шесть.
Этот случай рассматривается в теореме путем изменения переменной x. Людмила Фирмаль
- Если мы суммируем эти неравенства от k = 1 до k = n、 2 / (^T / ( * ) ^ 2 /(A + 1). 6 = 1 1 6 = 1 Вы будете иметь Н + 1 2 НК) 6 = 1 «»5 = 5 НХ) ух ^ 8н + 1-Н1),= = 1, 2、 (35.28)) И предположения Если Интеграл (35.27) сходится, то по 33.3 Лемме 1, n = 1, 2,… П \ −1 СОТРУДНИЧЕСТВА 5 /(х) УГ $ [(х) ух. 1-1 Отсюда и неравенство(35.28)、 4-и 5Н+ 1 = ^ /(1)+ $ /(х)Д、 35.7.Интегральная сходимость ряда 563. То есть, поскольку подпоследовательность ряда (35.26) ограничена вершиной, согласно предыдущей теореме, этот ряд сходится. Если ряд (35.26) сходится, и его сумма равна 5, то согласно той же теореме все η-1, 2,…Для 5π= 5, а следовательно, и для всех η= 1 по неравенству (35.17), 2…、 Л+ * $ 1 (х) ух ^ 8. Один Где если^ 5 = 1, если принять η за η> 1, то неотрицательной функцией/ 6р §/(х) т ^ ^(х) ух ^ 8. 1-1 Шесть.
- Итак, совокупность всех интегралов. § / (x) Я Вышеприведенный член и, следовательно, Интеграл (35.27) сходятся (см. лемму 3 в§ 33.3 1). Я не уверен. Это значительно облегчает исследование сходимости рядов, так как можно использовать аппарат интегрального исчисления, разработанный в предыдущей главе, когда можно выбрать функцию, соответствующую заданному ряду и, следовательно, свести задачу изучения сходимости рядов к исследованию сходимости интегралов. Образцы. 1.Просмотрите серию еще раз (см.§ 35.3) 1 + 2 ^ + sz+•••+ ±••(35.13) n-й член un = \ / pa, n = 1, 2、 В этом случае легко выбрать функцию f (x), указанную в теореме. Hx)= ^ m, x ^ 1. 4 CO Потому что интеграл^ сходится на 1 и расходится на 1 ae1, то ряд(35.13) сходится на 1 и расходится на 1.
Как видно из вышеизложенного, применение к исследованию ряда интегрального критерия сходимости ряда значительно упростило задачу изучения сходимости этого ряда. Людмила Фирмаль
- Эти факты были установлены ранее другим методом в разделе 35.3(см. примеры 1 и 2 там).§ 35.Числовой ряд 564. 2.Рассмотрим серию И 2(л + 1)1П(П + 1) ’(35.29) Н = 1 Этот ряд легко исследовать с помощью интеграла. И Г-ых (+1) 1П( + 1) Признак сближения. Неотъемлемый\ 4-и = Когда ^ расходится, ряд (35.29) расходится. 1П 2 Следствием теоремы 10 является то, что она проста, но часто полезна в приложениях, которые объясняют 1 вещь. если существует естественное nn такое, что неотрицательная функция / убывает при x> n0, то ряд Да. н = по Сходятся только тогда, когда Интеграл сходится 4-и ^!(х) ых. = y + n0-1. И 4. В 1 час п 1П » п ’ 7. 2 капли ВН * + А2(а = сопи! Е/?это не. н-2 Н-1 «В 2» л! е-2 Н-1 ’•2(1Агентство Н = 1 3 ″ л! х. ^ северный л = 1 «+!»/ ’2П + 1 Н-1 Упражнение. Исследуйте сходимость ряда. 10. Вы хотите быть 0 r C? 1.Серия P + Y2 + P3+ 0 * ±это отличный способ доказать, что вы хороший человек. И. Сходится золото используйте p-i2p-1 11. 0.^ 1.1, чтобы доказать его ряд. 1 1 1.с 1 У + 2?+ ^ + ^ + Сходится, Пт-2П = ко.
Смотрите также:

