Оглавление:






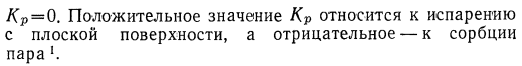

Интегральные уравнения диффузионного пограничного слоя
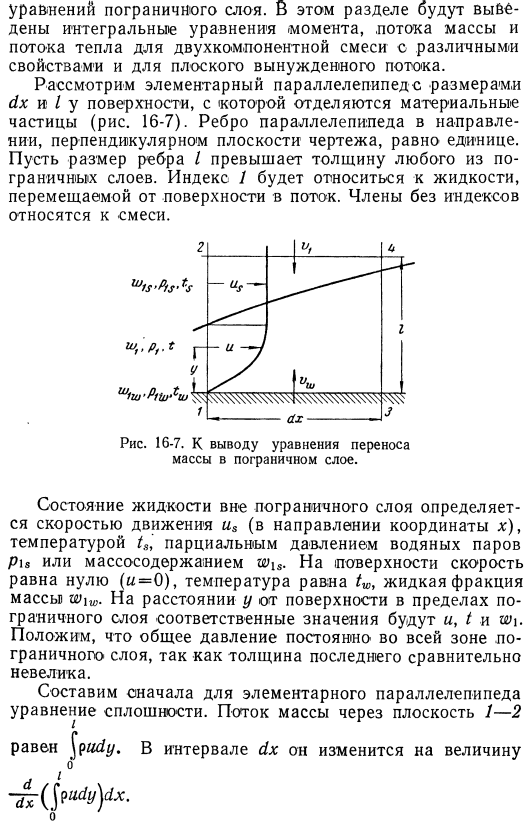
- Во многих случаях приближенное преобразование, основанное на интегральных уравнениях пограничного слоя, приводит к результату, а не к точному решению Уравнение границы layer. In в этом разделе мы выберем 2-компонентные смеси с различными свойствами и интегральными уравнениями для момента, массового расхода и теплового потока для плоских вынужденных течений. Рассмотрим базовый параллелепипед с размерами dx и i, на поверхности которого разделены частицы материала (рис. 16-7).
Края коробки в направлении, перпендикулярном плоскости чертежа, будут равны 1. Предположим, что размер ребра превышает толщину пограничного слоя. Индекс 1 относится к жидкости, которая движется от поверхности к потоку. Члены без индекса относятся к смешиванию. Рисунок 16-7. To выведите уравнение массопереноса в пограничном слое. Состояние жидкости вне пограничного слоя определяется скоростью uₛ (направление координат x), температурой tₐ, парциальным давлением водяного пара или массовым содержанием.
Равновесные состояния термодинамических систем могут быть описаны с помощью небольшого числа макроскопических параметров, таких как температура, давление, плотность, концентрации компонентов и т. д. Людмила Фирмаль
Скорость на поверхности равна нулю (u = 0), температура равна tw, а жидкая доля массы равна w fractionw. At расстояние y от поверхности в пограничном слое, соответствующие значения и, t, и ah. Поскольку толщина пограничного слоя относительно невелика, предполагается, что полное давление является постоянным во всей зоне пограничного слоя. Во-первых, мы создаем основное параллелепипедное непрерывное уравнение. Массовый расход через плоскость 1-2 равен Уды.
Следующие значения для интервала ДХ d Я — ^ udyyx. О В стационарном режиме такое же количество должно дойти до коробки через плоскости 1-3 и 2-4. В плоскости 1-3 (на поверхности) наблюдается вертикальная скорость vwₜ. Его значение было определено в предыдущем разделе. Сделайте скорость частицы через плоскость 2-4 равной vₜ. Тогда условия непрерывности потребуют этого пуда-РС Фольксваген. Я д₽а= ^ Жо Отсюда мы получаем уравнение импульса (см. § 6-2). (16-25) Я. .(Р ^ ды-ПВ ^^- ^ — л ^ .О компании DX Используйте те же преобразования, что и уравнение неразрывности и члены 6-2 для получения интегрального уравнения движения .
Количество Я ^ (4ₛ-у) ^ Уды- — О (16-26) Через гуру ду1 .Дж (РА-Р») ау» Напряжение трения на поверхности определяется по формуле^ w = ^ w (du / dyjw .It выражается как градиент скорости в соответствии с полученным уравнением импульса отличается от уравнения (6-10) только термином Wvwuₛ .Для того чтобы сформулировать уравнение потока массы жидкости/, необходимо учитывать тот факт, что в стационарном режиме разность масс жидкости, осуществляемая плоскостью 1-2 и уносимая через плоскость 3-4, должна покрываться притоком масс через плоскости/-2 и 2-4 .
Равный массовому расходу жидкости на твердой поверхности к / нaа .И затем .Я .. Я. Да. Подставляя значение vₗf, определяемое из уравнения неразрывности (16-25) и записывая массовую долю вместо парциальной плотности, получаем: Я. .±J (a, |ₛ-w .что ?UD-vₐwₗₛ = mᵢw .Да .Заменяя массовую скорость пара mₗw на Формулу, определяемую формулой (16-8), она выглядит следующим образом: / Дж (^ 1 $» ^ 1) = ЛП ($ ’) * + (16-27) Уравнение теплового потока выводится таким же образом, то есть на основе теплового баланса основного объема .Если тепловой поток на единицу твердой поверхности равен £j * pcₚtudy-Pⱼcₚₛt $ Vₗ = QW .0 .Тепло передается от твердой поверхности не только теплопроводностью, но и конвекцией с компонентом 1 .
Следовательно、 с TV .Вт ПВ т£> з Вместо подстановки значений, определенных из уравнения неразрывности, получаем уравнение вида: •/ 4 — { (с т-с т) пуду = а (- 4- (с т-с т) п В .(іх, J В ’ / «П’ ’О’ ды разъема j1’ps с ПВ ж’ ’ ко Вт (16-28) Таким образом, уравнения диффузного пограничного слоя ( (16-26) и (16-28) отличаются от соответствующих уравнений теплопередачи только дополнительными членами скорости vw .
Эти уравнения соответствуют, как это было сделано в разделе 6-4 Приведены формулы для распределения скоростей, температур и массовых долей и последующего определения толщины границы layer .To для повышения точности этого приближенного решения полезно применять допустимые значения к фактическим условиям в качестве граничных условий используемой кривой распределения .В § 7-3 постоянство величины 2-й производной температуры относительно расстояния от твердой поверхности было установлено на основании того, что qw считается постоянной в непосредственной близости от стенки .
Для тепловых потоков при массообмене справедлива формула (16-28) .Ну-и в этом случае тепловой поток qw в непосредственной близости от стены должен иметь определенную value .So .Массовая скорость pwvw должна быть постоянной вблизи стенки .Формула (16-8) справедлива для массового расхода пара .При дифференцировании уравнения (16-8) оно выглядит следующим образом: (16-30) Формула (6-2) справедлива для напряжений трения rw без диффузии .Это уравнение изменяется, когда с поверхности происходит большой объем оттока .Представьте себе плоскость, расположенную параллельно твердой поверхности .
- Тогда в этой плоскости вязкость жидкости, движущейся вдоль поверхности, вызывает трение кроме того, эта плоскость имеет виртуальное напряжение трения, вызванное импульсом и движением массы, проходящей через плоскость .Такое напряжение трения уже рассматривалось в разделе 8-1 .— Следовательно, общее напряжение трения равно следующему .Т = — пт) » .(16-31) В этом случае напряжение трения должно быть постоянным вблизи стенки .Поэтому производная по отношению к y вблизи стенки должна быть равна нулю .
Если разность парциальных давлений в пограничном слое мала по сравнению со средним гидравлическим давлением, то расчет значительно упрощается .В этом случае скорость vw (перпендикулярная стенке) мала и пренебрежимо мала в уравнении (16-26) — (16-28) .Тогда уравнения для импульса (16-26) и теплового потока (16-28) примут тот же вид, что и для чистого теплообмена (см .Разделы 6-1 и 7-1) .Свойства, указанные в Формуле, являются, по сути, свойствами жидкости 2 .Последнее означает, что массоперенос не влияет .Формула теплопередачи (16-27) описывает процесс массопереноса, но решать ее не нужно, так как результат будет следующим: из аналогичных условий .
Термодинамика не рассматривает особенности строения тел на молекулярном уровне. Людмила Фирмаль
При решении описанных выше дифференциальных уравнений расчет массопереноса без теплообмена, когда среда движется вдоль плоскости в области ламинарного пограничного слоя, осуществляется по формуле Э .-В .Эккерта .Lilein [l . 283] и spalding (l . 284) для естественной конвекции в вертикальной пластине перед критической точкой сферы .Расчет проводится при парциальном давлении, превышающем массовое содержание, в предположении, что оба компонента являются газами .Расчет показывает, что массоперенос является функцией 2-х безразмерных величин .Первый: a — (d / v) x (mj / m), где d-коэффициент диффузии .
V-коэффициент кинематической вязкости; m-молекулярная масса парогазовой смеси для промывки поверхности испарения, mi-молекулярная масса жидкости, подлежащей испарению с плоскости, или жидкости, подлежащей поглощению плоскостью .При выводе приведенной формулы предполагалось, что молекулярные массы обоих компонентов незначительно отличаются друг от друга, поэтому величина а не должна существенно отличаться от числа Шмидта z) / v .2-я безразмерная величина Г___ П С П Ш П П Ш Представляет собой отношение разности парциальных давлений пара компонента 1 вне пограничного слоя .1 соображения сходства высказали Шмидт и нуссель том .Аккерман предложил приблизительную коррекцию высокого парциального давления (l . 282] .
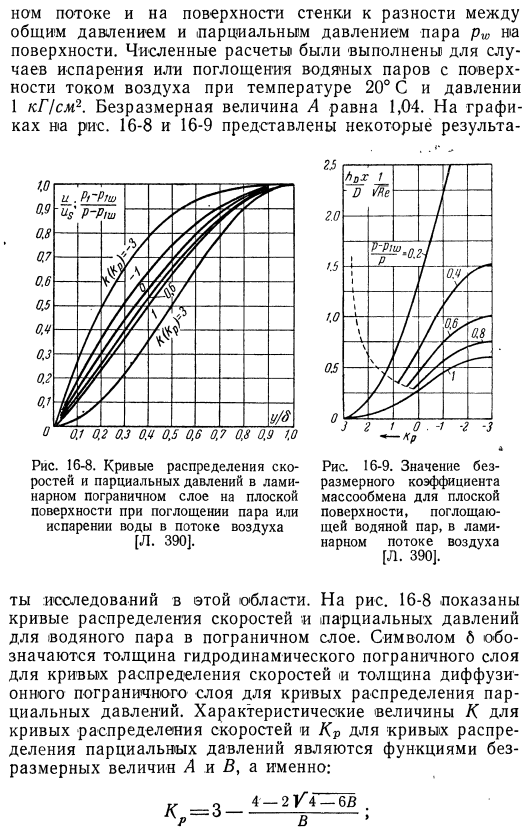
Численный расчет проводили для испарения или поглощения водяного пара с поверхности потоком воздуха температурой 20°с, давлением 1кг1см2 (разность между суммарным давлением потока и поверхностью стенки и давлением пара pw) .Безразмерное значение a равно 1 04 .Графики на рисунках 16-8 и 16-9 показывают некоторые результаты Рис .16-8 .Кривая распределения скорости и парциального давления ламинарного пограничного слоя на плоскости за счет поглощения пара или испарения влаги в воздушном потоке[l .[390] .И Рис .16-9 .Значение безразмерного коэффициента массопереноса плоскости, поглощающей водяной пар в ламинарном потоке[l .[390] .
Вы проводите исследования в этой области .На рис .16-8 показана кривая распределения скорости и парциального давления водяного пара в пограничном слое .Символ d обозначает толщину гидродинамического пограничного слоя кривой распределения скорости и толщину диффузного пограничного слоя кривой распределения давления .Характерные значения кривой распределения скорости и кривой распределения давления являются функциями безразмерных величин a и b .in другие слова、 4 2 В-4-6В Так .. К Джей-3Н (2- ^ 4-6В), а /iₚ Л. С. :(2-/ 4-66)3/3 ^-4 ′ Где 8-толщина гидродинамического пограничного слоя. 8 ^ — толщина диффузного пограничного слоя.
Соотношение 6 / dr равно 1 для испарения воды с плоской поверхности и увеличивается до 2 для поглощения пара плоской стенкой при существенной разнице парциального давления. Для массопереноса (испарения) с плоскости k положительна, а для сорбции-отрицательна. Кривая k = 0 отражает распределение скорости течения вдоль плоскости без массопереноса, а также распределение скорости и парциального давления при очень малых разностях парциального давления. Этот график показывает, что кривая распределения скорости и парциального давления сильно меняется в зависимости от разности парциальных давлений.
Кривая/ c = kp = 3 действительна, когда парциальное давление воздуха на поверхности zero. It происходит на 1 поверхности кипящей воды. Массовый расход от поверхности к поверхности можно определить из графика на рисунке. 16-9. Значение hd-это коэффициент массопереноса. В местах, где существует массовый поток вблизи поверхности, существует неопределенность в определении коэффициента переноса. Уравнения (16-23а) и (16-2336) соответственно представляют тепловой поток, обусловленный теплопроводностью и диффузионной массой flux.
To получить формулы для полного теплового потока и массового потока, конвективный поток должен быть рассмотрен. С другой стороны, определение, используемое в Формуле (16-23), имеет то преимущество, что коэффициент переноса, определенный таким образом, зависит от небольшого параметра. Коэффициент массопереноса 16-9 на рисунке показан весь массовый расход на поверхности пластины, выраженный уравнением ’ (16-8). Этот коэффициент hd, в дополнение к параметру yp, который представляет собой конвективную скорость vw, отношение давления (p-p w)! Обратите внимание, что это функция p.
Только кривые, которые находятся выше пунктирной кривой, имеют фактические физические значения. Значение коэффициента массопереноса при незначительной разнице парциальных давлений находится на вертикальной линии cr = o положительные значения комбинационного рассеяния относятся к испарению с плоскости, а отрицательные — к сорбции пара*.
Смотрите также:
| Диффузия | Подобие процессов массообмена и теплообмена |
| Ламинарный пограничный слой на плоской плите при переносе массы и тепла | Испарение воды в воздух |

