Оглавление:


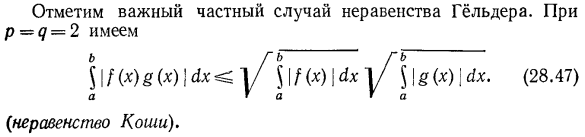

Интегральные неравенства Гёльдера и Минковского
Интегральные неравенства Гёльдера и Минковского.-1 + 1 = 1 п я (См. (20.49), (20.51) и (20.52).И затем… $!/(*) &(х) 1 ХХ=$; /(х) р (1х$) §(х)} (28.42) Я/? (28.43) Предположим, что функции/и^определены в интервале[a, 6], 1 p C + oe, они интегрируемы, а число g определяется уравнением. 1 Р 1 / п 1 $ /(1 + 3Р(1!П\^ $} (х)\ РХ + \ \ §(х)\ р (1×1 / п (28.44) (Неравенство Гельдера) (Неравенство Минковского). СЧ Нет? $ 1 /(1 Реф 1 / п ВТОРОЙ ^ Ч » Смотрите! 1/4 (28.45)) Давайте докажем это inequalities.
Г. Минковский(1864-1906) родился в России и работал в Швейцарии и Германии. Людмила Фирмаль
- It вводит обозначения, чтобы быть кратким Неравенство (20.53)) а> 0, b2r0、 И^ АП. БЖ АО в * ’О. Л. Гельдер (1859-1937) немецкий математик. ** 1 / я Если левая сторона этого неравенства равна нулю, то неравенство (28.44) очевидно истинно, а если оно не равно нулю, то обе стороны неравенства(28.46) уменьшаются в 1 раз. ] \ Т (х)+ 8 (х)\ ПВ 466. § 28.
- Свойства интегрируемой функции Я положу его туда. !/(*)! 18(х) я [си.] 1 / 1У ’ 1В!«’ Тогда любой x e [a, b] ! / ( * ) I I I ^ ( * ) [^1 I! (х) -\ р 1 я ^(Г)!? 1/1 п шрр Интегрируем это неравенство с интервалом[a, 6] и используем (28.45) и (28.42), чтобы、 П5, мг ( ’) [‘б’] Так… п; / л То есть доказано неравенство (28.44). Докажем неравенство (28.44).Проверка неравенства проста. 51 /(x)+ 8 (X)!Пакс = 51 /(х)+ я(Х)|] /(Х)+§(х)| П-Х 5! /(*)! Я / ( * ) + 8 (х) Т1 ух + $ 18 (х) [я /(х)+§(х)[П-1 ух. Но.
Примените неравенство Холдера к каждому из полученных интегралов. Людмила Фирмаль
- Отметив g (p-1)= p (см. (28.42)). 1!П \ б 51 / ( * ) + Д ()\ П ЛК 51 /(х) я «ух $ 1 /(х)+ е(х)|» (п-х) ух 1 / п [б] 1 / я + + 5!8 (х)!Пи \ \ 1(х)+§(х) {^п-xyx \ СХ) \ богатый 1 / п К 1 ^() м * 1 / п) } $ Я… Я?(Х)+8 (х)\ РХ ОЗМР 。 (28.46) , По отношению(28.42)、 Свадьба Минковского. Ноль 29.1.Непрерывность интегралов относительно верхней границы Внимание к существенному конкретному случаю неравенства Гельдера.Четыреста шестьдесят семь для Р = 7 = 2 ГБ А / \ \ НХ)\&ХД/) \§(х) \ ДХ. (28.47) а г а * а {Неравенство Коши).
Смотрите также:

