Оглавление:


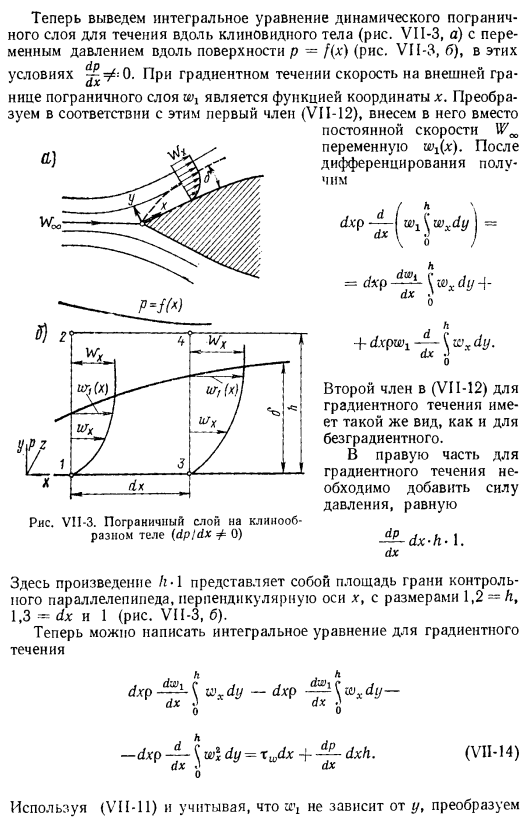







Интегральное уравнение динамического пограничного слоя
- Если давление и скорость вдоль пограничного слоя (X-координата) не изменяются, т. е. — = 0 и=^=, то получаем интегральное уравнение для случая несжимаемой жидкости (p = const), протекающей в направлении пластины (dp / dx = 0), т. е. const (рис. VI1-2). размеры в направлении оси x (вдоль пограничного слоя) dx, осевой / / размер h и объем h выбираются всегда больше толщины пограничного слоя 6 и толщины главной оси (вдоль оси Z) в dx. Примените закон импульса к течению пограничного слоя.
Этот закон означает, что изменение импульса (массы скорости) выбранного параллелепипеда за единицу времени в общем случае равно сумме сил массы (гравитации) и поверхности (давления и трения), действующих на параллелепипед. Массовая сила и давление будут zero. So, в рассматриваемом случае изменение момента движения параллелепипеда равно приложенной к нему силе трения.
Коробки уменьшают цены вдоль оси x Рис VII-2.To вывод интегрального уравнения динамического пограничного слоя. Людмила Фирмаль
Основываясь на следующих рассуждениях, найдите изменение импульса. Массовый расход от плоскости 12 (рис. VII-2)до параллелепипеда равен л. Да. Если массовый расход через поверхность 34 больше, чем через поверхность/ 2, то разница в стоимости через эти поверхности положительна、 л \ (ля) В результате Величина положительного разностного движения-P ^ {нет. ды ^ ДХ- б).
Массовый расход через плоскость 34 больше, чем через плоскость 12, но рассматривается несжимаемая жидкость, и это возможно только в том случае, если разница в расходе через плоскости 24 и 34 (а) параллелепипеда является такой ситуацией. Эта жидкость вводит параллелепипед с импульсом, который можно определить по формуле: Расход жидкости в количестве, равном (с).
Ну и в соответствии с законом О величине перемещения рассматриваемого корпуса с учетом силы трения、 Я умею писать. П ^ я ДХ-ДХ = xwdx(ВИ1-12) Или после простого преобразования (ich — (VII-13) dx J p Полученное интегральное уравнение также называется интегральным соотношением Калмана ограниченного неградиентного потока= o). Теперь в этих условиях выведем интегральное уравнение для динамического пограничного слоя клиновидного объекта (рис. VI1-3, а) с переменным давлением вдоль поверхности p-f (x) (рис. VI1-3, .
Б) -=/: 0. в градиентном потоке скорость на внешней границе пограничного слоя является функцией x coordinate. In в соответствии с этим мы преобразуем первый член(VI1-12) и вводим переменную wjx вместо постоянной скорости).После дифференциации, получить 2-й член (VI1-12) для градиентного потока имеет ту же форму, что и для без градиента. В соответствующей части градиентного потока давление должно быть равно — ДХ-х-1. дуплексный. Где продукт / g-1 представляет собой площадь лицевой поверхности блока управления, перпендикулярную оси X размеров 1.2-h, 1.3 = s / x и 1(см. рис. VII-3, b).
Теперь мы можем написать интегральное уравнение градиентного течения (В VII-14) Используйте (VII-11) и преобразуйте, учитывая, что он не зависит от y Последние условия (VI1-14) являются: Заменить (VII-14) вместо значений из полученной формулы и уменьшить、 ООО. А, Л Ж-Л \ ДГ = — Р ДХ о р Сгруппируйте первую и 4-ю части полученного уравнения, затем 2-ю и 3-ю части — Ф ([£?!- Wₓ) wdydy+wₓ) dy =. (VII-I5) с DXL ДХ 3 П .
В обоих интегралах полученных уравнений подынтегральная функция на внешней стороне пограничного слоя равна нулю, так как скорость w, входит, так что любое число oo может быть принято за верхний предел, и уравнение (VI1-15)остается справедливым. Я введу обозначения (VII-I6) (Значение 6 *также называется сжатая толщина) и Да. (Величина 6 * * называется толщиной потерь с учетом вида формулы (VI1-15) (mi * 6) 4-i0j __ дуплексный. п. (VI1-17) И М П У Л А) (В VII-18) Уравнение (VII-15) или (VII-18) называется плоским несжимаемым интегральным уравнением пограничного слоя с градиентом давления.
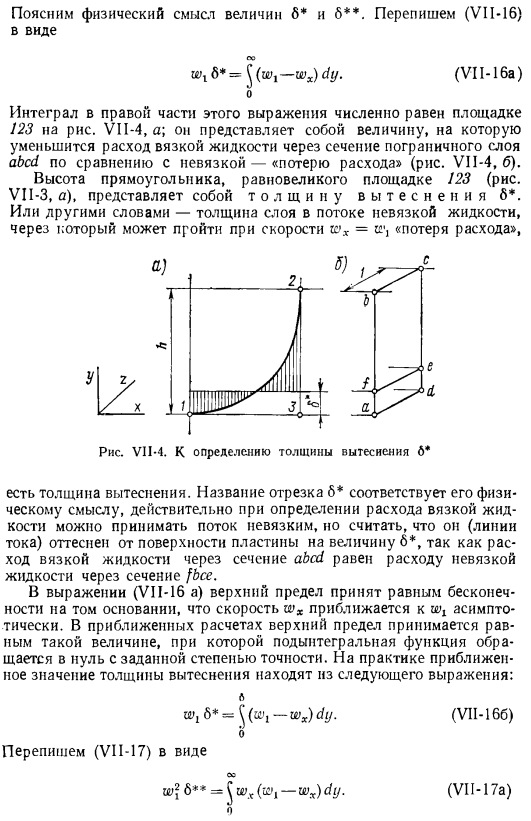
Поясним физический смысл величин 6 и 6. Перепишите в виде (VI1-16) wₗ д = ^(w₁-wₓ)ды. (ВИ1-16а) О Интеграл справа от этого выражения численно равен области 123 на рисунке 1. VI1-4, а; он представляет собой величину, на которую уменьшается расход вязкой жидкости через поперечное сечение пограничного слоя, по сравнению с невязкой «потерей потока» (рис. VII-4, 6). 123 (рис. VII-3, А) и высота прямоугольника той же площади представляет собой толщину экструзии 6*.Или другими словами-скорость=и ’толщина слоя потока невязкой жидкости, которая может проходить через» потери потока»、 Существует толщина экструзии.
Название сегмента 6 * соответствует его физическому виду meaning. In факт, при определении расхода вязкой жидкости может быть взят невязкий поток, но предполагается, что (линия потока) выталкивается из поверхности пластины на 6*. через раздел fbce. В Формуле (VI1-16 a) верхняя граница равна бесконечности по той причине, что скорость wₓ приближается asymptotically. In приближенный расчет, верхняя граница предполагается такой, что подынтегральная функция исчезает с заданным precision. In на практике приблизительное значение толщины смещения определяется по формуле: л. — [0ₓ) телетайп. (В VII-166) О.
Перепишите в виде (VI1-17) И & У2 6 ** = jjwₓ(в ^ — wjdy. О (VII-17а) Поскольку формулы (VII-16 А) и (VII-17 а) основаны на одном и том же принципе, для величины 6** можно дать следующее определение: толщина слоя в потоке невязкой жидкости, через который проходит импульс, равна потере импульса вязкой жидкостью при протекании через пограничный слой и называется толщиной потери импульса (импульса). Прежде чем приступить к решению интегрального соотношения пограничных слоев, отметим следующие важные ситуации.
При решении дифференциального уравнения пограничного слоя (VI1-10) эта функция выбирается произвольно при решении интегральной функции (VII-13, VII-15), если искомой функцией является= / ’ ( * / ) распределения продольной скорости wₓ относительно толщины пограничного слоя. Однако он обеспечивает выполнение граничных условий на поверхности тела и внешней кромке пограничного слоя. Опыт показал, что течение в пограничном слое является ламинарным или турбулентным. Видно, что интеграционное соотношение подходит для обоих режимов течения, но форма функции (!/).
Их выбор, как и метод определения касательных напряжений (правая часть интегрального соотношения), зависит от ламинарной и турбулентной обстановки. Поэтому рассмотрим решение интегрального соотношения этих 2 режимов течения отдельно. Решение интегрального уравнения для динамического ламинарного пограничного слоя Рассмотрим плоскопараллельный поток жидкости, который течет в продольном направлении вокруг пластины. Пограничный слой возникает на передней кромке пластины, а его толщина вдоль оси Х постепенно увеличивается(рис. ВИ1-5).
- Как показывает опыт, в начале пластины появляется ламинарный пограничный слой, наблюдается ламинарное движение потока. Ламинарное движение-это движение, в котором возможно существование стационарной орбиты частицы. на определенном расстоянии от передней кромки пластины hcr ламинарный пограничный слой постепенно начинает переходить в турбулентность, и в последней наблюдается движение турбулентной жидкости.
Турбулентность m-это движение жидкости, в которой траектория движения частиц изменяется случайным образом со временем, а нерегулярные пульсации скорости, давления и других параметров возникают в потоке и распределяются неравномерно в потоке (v174). Экспериментально установлено, что переход от ламинарного режима пограничного слоя к турбулентности происходит при определенном значении x. Число Рейнольдса ReKₚ= * украинское. Это называется критическим.
Требуемым значением является толщина пограничного слоя . Людмила Фирмаль
Однако, если основная турбулентность искусственно возбуждается, например, выставляя сетку перед пластиной или увеличивая турбулентность в самом пограничном слое, переход может начаться с меньшим числом Рейнольдса, чем ReKₚ. Например, сделайте поверхность плиты шероховатой. Напротив, можно задержать переход от ламинарной к турбулентной области пограничного слоя и устранить источники турбулентности как в основном потоке, так и в самом пограничном слое.
Проблема турбулентности будет рассмотрена более подробно позже. Решите интегральное соотношение ламинарного пограничного слоя на пластине. 6.Рассмотрим решение формулы (VI1-13).Это эффективно, если давление вдоль пограничного слоя не изменяется. (VI1-13) интеграция принимает верхнюю границу. Рисунок VI1-5.Ламинарные и турбулентные поперечные слои на пластине в вертикальном потоке .
Условие(г = Б, ЗП = Т£.сумма потерь подынтегрального выражения с точностью, указанной в (I), равна y-b. тогда интегральное соотношение (VII-13) принимает вид: — ±- (Wᵢ-Wₓ) Wdydy=(VII-19) дуплексный. Джей Пи. Выберите полиномиальную форму функции распределения скорости wₓ по толщине пограничного слоя = а 4-х 4 — Су * + диф (в VII-20) Где a, b, c, d-постоянные коэффициенты. Для определения постоянного коэффициента (VI1-20) используются условия поверхности пластины y = 0 и внешней границы y-6 пограничного слоя. Так… Г = О, а> Х = О-Е-Л = О、 2-я производная равна нулю (в данном случае dp! dx = G) является производным от первого выражения (VI1-10). если y = 0, то все члены, кроме последнего, исчезают.
Так… г-м и WN = 1 ^ 00 = const и-^ = 0、 Я буду. Исходя из предположения о плавном переходе к вертикальной линии кривой w y = f (y)= const, 1-я производная равна нулю. Внешняя граница пограничного слоя (см. Рисунок VI1-2). если вы установите y = 0 и w = 0, вы получите a = 0 из (VI1-20).1-я производная от (V1I-20) является ^ — =б + 2cy + 3д-г \ ды Второй. = 2cdy + БР-ыды = 0. почтовый индекс dy2. Сделайте вторую производную равной нулю 2С 4-(м-м = 0、 если y = 0, то c = 0. Если приравнять первую производную к нулю и считать c-0 и y = 6、 b + W-0, 6 = — 3J62. используйте вам значений A, C и B, где Y = 6 и 1 Если №. «=- 3J634-D63, как, Д= -.
Используя значения констант a, b, c, d, полученные по формуле (VII-20), находим искомую функцию распределения продольной скорости bj по толщине пограничного слоя. wₓ3 г 1 найти. 2 6 2 {6 J (В VII-21) I3 V>(V VI V 2 6 2 1 x использование 0. , i)’] X 39 1PL 280. И Подставляя найденную зависимость в интеграл от импульса (VI1-19), получим: Л4. ’4-ч — + — и Используя зависимость (VI1-21), найти напряжение сдвига y = O на поверхности пластины. \ do 4 = o 2 6 (VI1-22).
Интегральное соотношение пограничного слоя (VI1-19), учитывающее последние 2 зависимости, будет представлять собой дифференциальные уравнения вида: _3?_7 =WW°°. 280 ДХ 2р 6 После разделения переменных, редукции, преобразования、 Расположите начало координат на передней кромке пластины, чтобы получить граничные условия в виде: Если мы интегрируем дифференциальное уравнение, которое мы приняли во внимание граничные условия、 6. 4.64 4.64 Икс Функция (VII-23) является приближенным решением дифференциального уравнения пограничного слоя без градиента давления в ламинарном режиме(VI1-10).
Сравните приблизительное решение с точным решением. Найти безразмерное напряжение сдвига. По этой причине разделите правую и левую части (VI1-22) на pU / t (см., например, Ш-18) и замените значение на 6 вместо (VI1-23). в результате вы получите формулу для определения безразмерного напряжения сдвига Аналогичная формула получена на основе точного решения и содержит численный коэффициент 0,332.Поэтому погрешность составляет всего 3 процента. Понятие локального коэффициента трения c}представлено в следующем виде. тай>(*) (В VII-25) Где Tc, (x) — напряжение сдвига пластины на расстоянии x от передней кромки.
Из приведенного уравнения (VI1-25), (VI1-24)、 0.646. (В VII-26) На основе точного решения уравнений пограничного слоя получено следующее уравнение для определения cf: 0.664. 1 Re * (VI1-27) Среднее значение коэффициента трения всей пластины длины I и ширины 1 определяется по формуле И затем… Или (В VII-28) Уравнение (VI1-28) представляет собой содержание закона Блазиуса для сопротивления вертикально обтекаемой пластины при ламинарном течении в пограничном слое поверхности.
Этот закон справедлив для числа Рейнольдса. Я… Ре / ₌ — 5-10 * — 10⁶. В заключение отметим основные особенности аппроксимационного метода решения уравнений динамического пограничного слоя. Основной предпосылкой метода аппроксимации является отказ от удовлетворения дифференциального уравнения пограничного слоя для каждой струйки жидкости в нем. Приближенный метод решает интегральную зависимость пограничного слоя, а не дифференциальное уравнение, так что дифференциальное уравнение может быть выполнено только в среднем по толщине пограничного слоя.
Точное решение дифференциального уравнения (включая пограничный слой) представляет собой функцию, которая при подстановке в это уравнение преобразует последнее в тождество любой точки исследуемой области (включая пограничный слой).Решение, полученное приближенным методом, не удовлетворяет этому требованию по вышеуказанным причинам. В методе аппроксимации поперечная составляющая скорости .
исключается из рассмотрения, так как учитывается только основное движение. Например, для плоскопараллельного течения учитывается основное движение вдоль оси x, и только скорость wₓ входит в интегральные соотношения (VII-13) и (VI1-15). В методе аппроксимации скорость через пограничный слой определяется на обоих концах интервала граничными условиями, поэтому она представляется произвольно выбранной аппроксимацией, которая является интерполяционной функцией.
Смотрите также:
| Исследование теплоотдачи методами теории пограничного слоя | Уравнение энергии для пограничного слоя |
| Уравнения динамического пограничного слоя | Интегральное уравнение энергии для пограничного слоя |

