Оглавление:



Интеграл по простому замкнутому контуру
- Интеграция на простом замкнутом контуре. Формула Грина позволит нам легко исчерпать вопрос о Кривом Интеграле второго типа, который мы только что затронули, проходя в§2 Главы XX. Некоторые
домены(2?() Дана непрерывная функция p (x, y) и (^(x, y). Давайте сначала рассмотрим вопрос о жилье — §4. Независимое условие криволинейного интеграла 265 Институт интеграции Р ых
Оде (Б Простая замкнутая схема-формула Грина должна присутствовать в Людмила Фирмаль
(E). -Этого мало:все равно надо Помещение Д5-Р и у н о ду ДХ (Е) лежа на RU*)(-я) *) Все кривые, упомянутые в этом пункте, считаются кусочно-гладкими. С учетом использования дополнительных производных контур (1), область (E) принадлежали каждый раз, и
область (O) была ограничена снаружи этим контуром. Другими словами, область (е) не должна иметь»дыр», а должна быть ровной. Область соединения с этим свойством называется областью соединения. Если мы говорим о конечной области, то есть если мы не
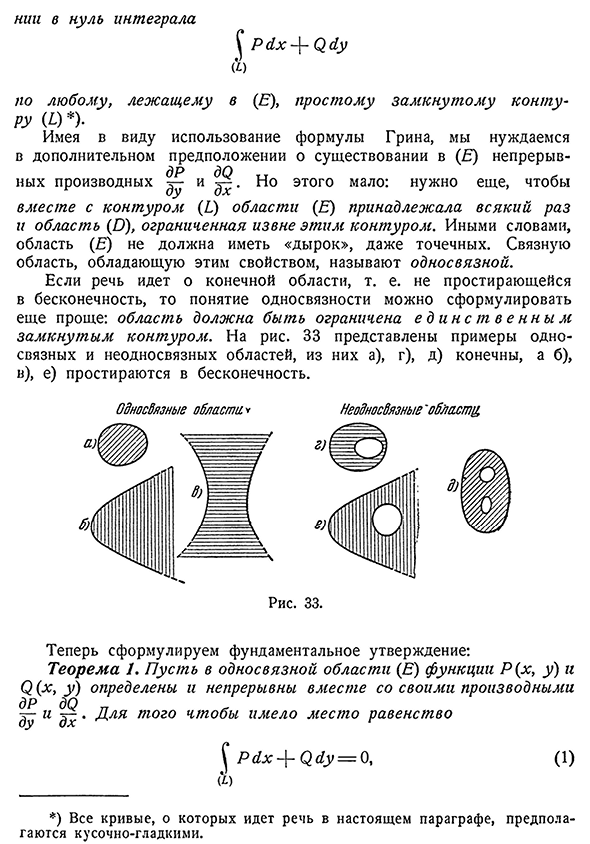
- расширяем ее до бесконечности, то понятие единства может быть далее легко сформулировано. Для риса. 33 Соединенные и несвязанные области, от б), д) простирающиеся до бесконечности. примеры a), d), e) конечны и b), Не подключен» , Здесь мы формулируем основное утверждение: теорема 1. Просто определите
функции P (x, y) и C} (x, y) в Связной области (E) и определите их производные Dr и d (?). . Для знака равенства P(1x~-=(1) делается) ( ^ ) 266 глава XXI. двойной Интеграл[349 Независимо от того, что простой замкнутый контур (E) в области(E\необходим, и достаточно того, что (E) эквивалентно Du~~DX * * ) Читатель может легко подтвердить, что условия (а) выполнены (Пример 1) и (4) n°333,
а (Пример 2), (3) и (5) — нет. (И) Фактически, согласно формуле Грина, равенство (1) Людмила Фирмаль
эквивалентно равенству (2) Условия его осуществления (а) ясны. Для доказательства и необходимости мы предполагаем, что равенство (2) всегда истинно. Дифференцируя интегралы по области [n°342], мы приходим к выводу, что в(E)тождественно, учитывая непрерывность функции частичной плотности т р р д± — d0_ph делать* » не ДХ *
Смотрите также:
Решение задач по математическому анализу
| Вывод формулы Грина | Интеграл по кривой, соединяющей две произвольные точки |
| Выражение площади с помощью криволинейных интегралов | Связь с вопросом о точном дифференциале |

