Оглавление:
Интеграл Коши. Интегральная формула Коши
Теорема 75.2. Пусть функция  аналитична в замкнутой односвязной области
аналитична в замкнутой односвязной области 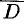 и
и  — граница области
— граница области  . Тогда имеет место формула
. Тогда имеет место формула
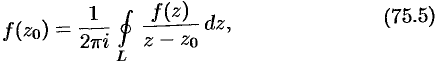
где 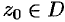 — любая точка внутри области
— любая точка внутри области  , а интегрирование по контуру
, а интегрирование по контуру  производится в положительном направлении (т. е. против часовой стрелки).
производится в положительном направлении (т. е. против часовой стрелки).
Интеграл, находящийся в правой части равенства (75.5), называется интегралом Коши, а сама эта формула называется интегральной формулой, Коши.
Формула Коши (75.5) является одной из важнейших в теории функций комплексного переменного. Она позволяет находить значения аналитической функции  в любой точке
в любой точке  , лежащей внутри области
, лежащей внутри области  через ее значения на границе этой области.
через ее значения на границе этой области.
Построим окружность 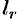 с центром в точке
с центром в точке  , взяв радиус
, взяв радиус 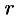 столь малым, чтобы данная окружность была расположена внутри области (чтобы
столь малым, чтобы данная окружность была расположена внутри области (чтобы 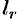 не пересекала
не пересекала  ).
).
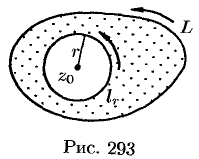
Получим двусвязную область 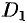 (заштрихованную на рис. 293), ограниченную контурами
(заштрихованную на рис. 293), ограниченную контурами  и
и 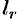 , в которой функция
, в которой функция 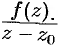 аналитична.
аналитична.
Тогда, согласно замечанию к теореме Коши (с. 545), имеем:
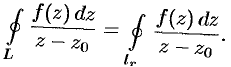
Отсюда следует:
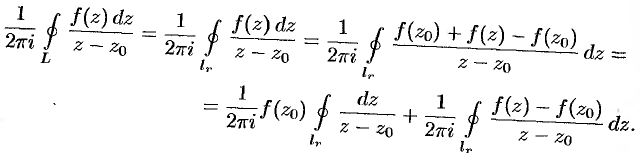
Но 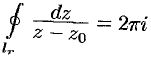 (см. пример 75.2). Следовательно,
(см. пример 75.2). Следовательно,
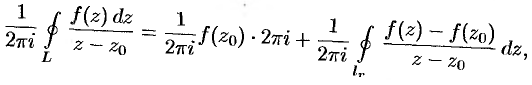
т.е.
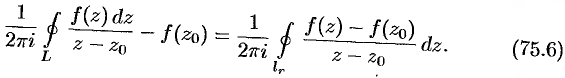
Оценим разность в левой части равенства (75.6). Так как аналитическая функция  непрерывна в точке
непрерывна в точке 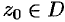 , то для любого числа
, то для любого числа 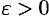 найдется число
найдется число 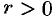 такое, что при
такое, что при 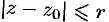 (на окружности
(на окружности 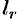 имеем
имеем 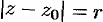 ) справедливо неравенство
) справедливо неравенство 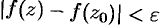 .
.
Применяя свойство 6 об оценке модуля интеграла (п. 75.1), имеем:
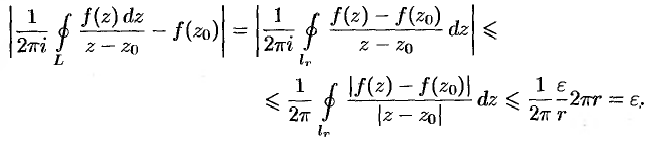
Так как 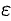 может быть выбран сколь угодно малым, а левая часть последнего неравенства не зависит от
может быть выбран сколь угодно малым, а левая часть последнего неравенства не зависит от 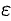 , то она равна нулю:
, то она равна нулю:
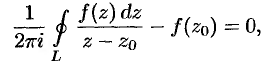
откуда следует формула (75.5).
Отметим, что интегральная формула Коши (75.5) справедлива и для многосвязной области: каждый из контуров обходится так, чтобы область  оставалась слева.
оставалась слева.
Применяя интегральную формулу Коши, можно доказать следующие теоремы-следствия.
Теорема 75.3. Для всякой дифференцируемой в точке  функции
функции  существуют производные всех порядков, причем
существуют производные всех порядков, причем  -я производная имеет вид:
-я производная имеет вид:
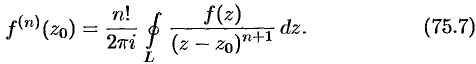
Теорема 75.4. В окрестности каждой точки  , где существует производная
, где существует производная 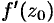 , функция
, функция  может быть представлена сходящимся рядом:
может быть представлена сходящимся рядом:
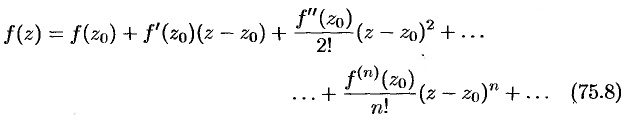
Таким образом, производная аналитической функции также является аналитической функцией.
Напомним, что из дифференцируемости действительной функции не следует даже существования второй производной (функция 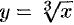 имеет производную в точке
имеет производную в точке 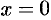 , а производная этой функции
, а производная этой функции 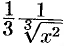 при
при 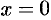 не существует).
не существует).
Ряд (75.8) называется рядом Тейлора функции  в точке
в точке  .
.
Ряд Тейлора дифференцируемой в точке  функции существует и сходится к самой функции. Ряд же Тейлора для действительной функции
функции существует и сходится к самой функции. Ряд же Тейлора для действительной функции  может сходиться к другой функции или быть расходящимся.
может сходиться к другой функции или быть расходящимся.
Замечание. Формула  -й производной функции
-й производной функции  может быть получена из формулы Коши
может быть получена из формулы Коши
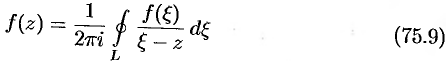
(в формуле (75.5) заменено  на
на 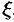 ,
,  на
на  ) путем последовательного дифференцирования равенства (75.9) по
) путем последовательного дифференцирования равенства (75.9) по  :
:
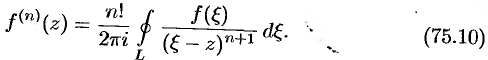
Формулы (75.5) и (75.7) можно использовать для вычисления интегралов по замкнутым контурам.
Пример №75.3.
Вычислить 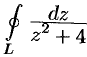 , где а)
, где а)  — окружность
— окружность
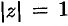 , б)
, б)  — окружность
— окружность 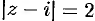 .
.
Решение:
а) функция 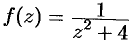 является аналитической в области
является аналитической в области 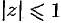 . В силу теоремы Коши имеем
. В силу теоремы Коши имеем 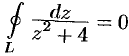 .
.
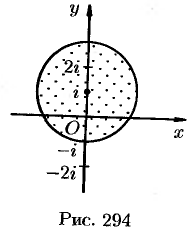
б) На рисунке 294 представлена область,
ограниченная контуром интегрирования.
В этой области 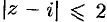 находится точка
находится точка 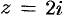 , в которой знаменатель подынтегральной функции равен нулю. Перепишем интеграл в виде
, в которой знаменатель подынтегральной функции равен нулю. Перепишем интеграл в виде
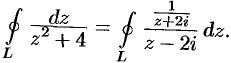
Функция 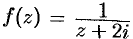 является аналитической в данной области. Применяя интегральную формулу Коши (75.5), находим:
является аналитической в данной области. Применяя интегральную формулу Коши (75.5), находим:
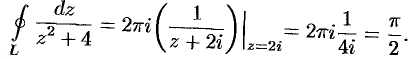
Пример №75.4.
Вычислить 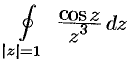 .
.
Решение:
Внутри круга и на его границе 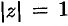 функция
функция 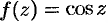 аналитична. Поэтому, в силу формулы (75.7), имеем
аналитична. Поэтому, в силу формулы (75.7), имеем
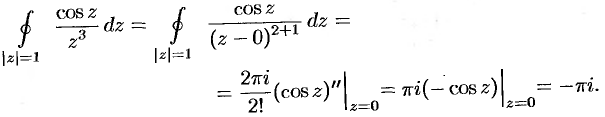
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интегрирование функции комплексного переменного |
| Интегральная теорема Коши |
| Нули аналитической функции |
| Классификация особых точек. Связь между нулем и полюсом функции |

