Оглавление:
Интеграл Фурье
Как известно, всякую (периодическую или непериодическую) функцию 
, удовлетворяющую на отрезке 
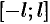условиям теоремы Дирихле, можно разложить в ряд Фурье
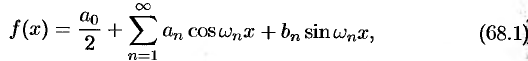
где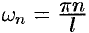 
,
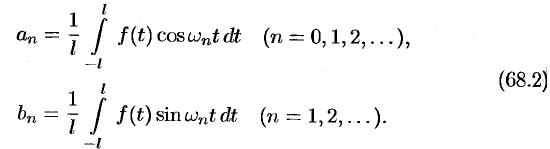
Это разложение будет справедливым на всей числовой оси 
в том случае, когда — периодическая функция с периодом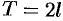 
.
Рассмотрим случай, когда — непериодическая функция, заданная на бесконечном промежутке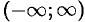 
(т. е. 
).
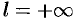Будем предполагать, что на любом конечном промежутке 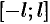функция удовлетворяет условиям теоремы Дирихле и что сходится следующий несобственный интеграл:
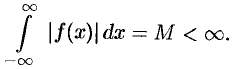
Говорят: абсолютно интегрируема на всей числовой оси.
Подставляя в ряд (68.1) значения коэффициентов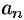 
и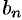 
(68.2), получим:
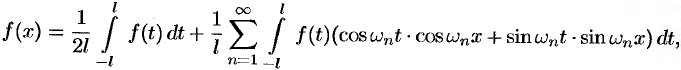
т.е.
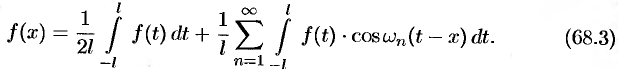
Будем теперь неограниченно увеличивать 
. Первое слагаемое в правой части равенства (68.3) при 
стремится к нулю, т. к.
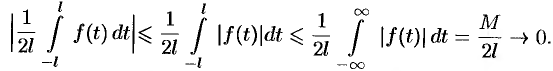
Рассмотрим второе слагаемое в равенстве (68.3). Величина 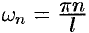принимает значения 
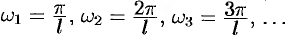, образующие бесконечную арифметическую прогрессию с разностью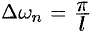 
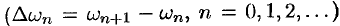, при этом 
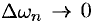при 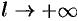. Итак,
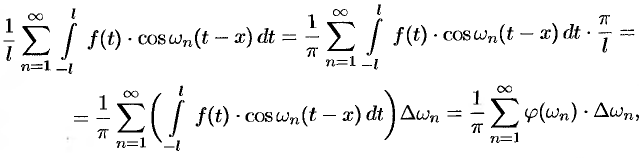
где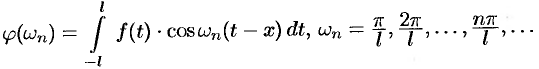 
Полученная сумма напоминает интегральную сумму для функции
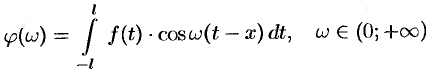
(доказывается, что так оно и есть), поэтому, переходя в равенстве (68.3) к пределу при 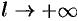, получаем
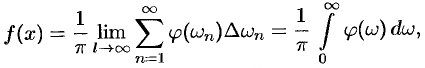
или
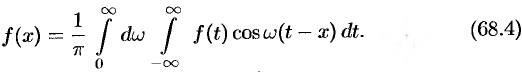
Формула (68.4) называется формулой Фурье, а интеграл в правой части формулы — интегралом Фурье для функции .
Формула Фурье имеет место в точках непрерывности функции ; в точках разрыва данной функции интеграл Фурье равен среднему арифметическому ее односторонних пределов:
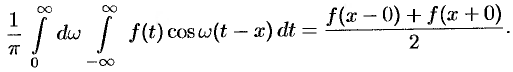
Формулу (68.4) можно переписать в другом виде (в виде однократного интеграла):
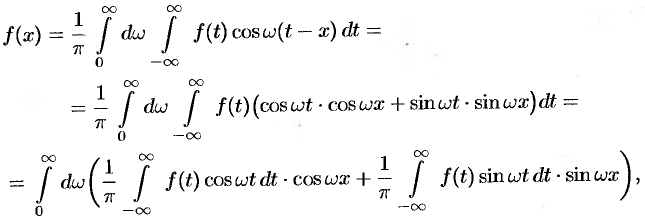
т.е.
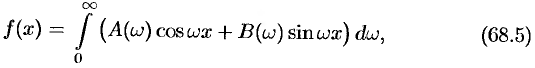
где
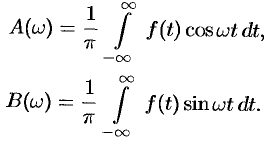
Как видно, есть аналогия между рядом Фурье и интегралом Фурье: в обоих случаях функция раскладывается на сумму гармонических составляющих. Однако, ряд Фурье суммируется по индексу 
, принимающему дискретные значения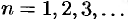 
, в интеграле Фурье производится интегрирование по непрерывной переменной 
.
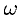Некоторые сведения, связанные с интегралом Фурье, изложим в виде замечаний.
Замечания.
1. Если функция — четная, то формула Фурье (68.5) принимает вид
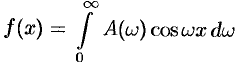, где 
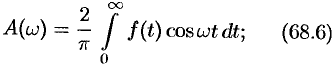
в случае нечетной функции —
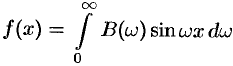, где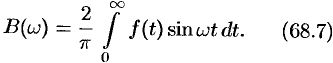 
2. Если функция Да;) задана лишь на промежутке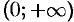 
, то ее можно продолжить на промежуток 
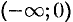разными способами, в частности — четным или нечетным образом: в первом случае она будет представлена формулой (68.6), во втором — формулой (68.7).
3. Формулу Фурье (68.5) можно представить в симметричной форме записи, если положить в формулах (68.6) и (68.7)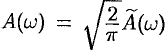 
, 
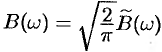. В случае четной функции
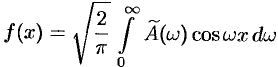, где 
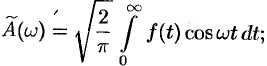
в случае нечетной функции
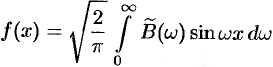, где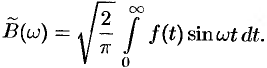 
Функци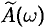и 
и 
называются соответственно косинус-преобразованием и синус-преобразованием Фурье для функции .
4. Интеграл Фурье (68.4) в комплексной форме имеет вид
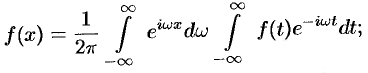
интеграл Фурье (68.5) имеет вид
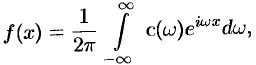
где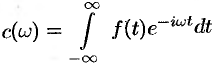 
; или в симметричной форме записи
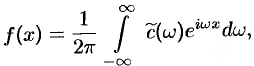
где
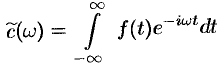
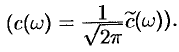
Пример №68.1.
Представить интегралом Фурье функцию
Решение:
Функция удовлетворяет условиям представимости интегралом Фурье, абсолютно интегрируема на промежутке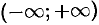 
:
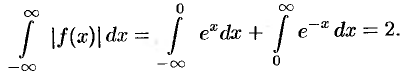
Функция нечетная, применим формулу (68.7):
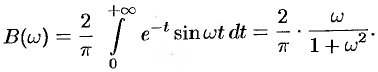
Следовательно,
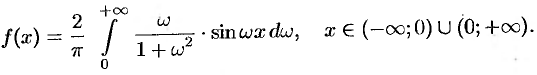
Замечание. Интересно отметить, что если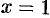 
, то
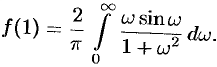
С другой стороны,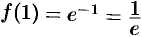 
. Таким образом,
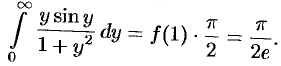
Иными словами, при помощи представления функций интегралом Фурье иногда можно вычислить величины несобственных интегралов.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Представление непериодической функции рядом Фурье |
| Комплексная форма ряда Фурье |
| Градиент скалярного поля и его свойства |
| Дивергенция поля. Формула Остроградского-Гаусса |
