Информация по Фишеру

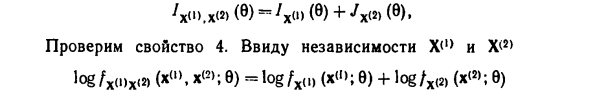
Информация по Фишеру

• Сначала предположим, что 0 — скалярный параметр. Просмотрите информацию о Kullback. = Wx; 6) log (/ (x; 0) // (x; 0 + Д0)) Лс, D2) Где dx = dx \ … dx ,, и интеграл понимается как i-мерный. Будете ли вы Поддержка всех основных P8, 0 ^ 9 является общей, Плотность f (x; d) должна удовлетворять свойству регулярности, Не указан, но содержит обоснование Срок действия следующего расчета. Развернуть логарифм Логарифмический член D2), формула Тейлора: D3) Где 0. / Находится между 6 и 0-rD0. Так как (мы рассматриваем журналы Натуральный логарифм) 180 | = — ^ — l = O, D4) Далее замена D3) на D2) * 10 г! V ae / «v; Но (см. D4) m ‘<> Y (X; 0) Cay (x; 0), .. 0

Таким образом, математические ожидания от обеих частей Уравнение D7), где x = X, Уравнение D8) определяет информацию Фишера для образца Xo Параметр 8 (при условии, что c — это интервал R]). в Вышеуказанное условие регулярности Выше расчета, информация Fnsher определяется по формуле D6) Откат информации со значением, близким к бесконечности Параметры fl и 8 + D8. Использование равенства (см. D4) M0 (<91og / (X; 0) / ab) = 0, D9) / (G) эквивалентное выражение I (Q) = DB (d \ ogf (\; 0) / q0). E0)

Используйте информацию о Фишере и всегда делайте предположения Предполагая, что равенство D9) выполнено, и гарантируем, что оно необходимо Людмила Фирмаль

Требования к соглашению о поддержке измерений и возможности дифференциации Дифференцирование D4) под знаком интеграла. 181 Уравнение E0, если статистическая модель дискретна) Заменяется на: Это требует равенства, как в D9). Параметр вектора 6 = @i, …, 0l), предполагается Предположим, что 0 является областью Rh. Информационная матрица Фишера Называется ковариационная матрица случайного вектора / (8) dlog / (X; 9) / dG *), E2) X имеет распределение Pe. Предполагается, Ожидаемое значение вектора E2) равно нулю: M02radelog / (X; 9) = .- 0,9 эВ, E3) Таким образом, * Ф) = Щ [(gradelog / (X; 9)) ‘gradelog (X; 9)]. E4) Информационная матрица Фишера определяется аналогично.

Для статистики T (x): / t bI E5) Где f (X) (t; 9) — плотность распределения T (X) в предположении. Предположение, что образец имеет распределение / (9) = / х (с). Если выборка статистики дискретна, плотность Е3) E4) и E5) заменяются распределениями вероятностей. Перечислите некоторые свойства информации Фишера. 1. Если T (X) — аналогичная статистика, fm (x> (9) = 0,6 эв. 2. Неравенство статистики T (X) ** fm (X) (c) , X <2>), XA>, X <2> -независимый Re, веб и Фишер конкретной информации. тогда Проверьте свойство 4. Учитывая независимость X <‘> и X <2) А). «B); c) = log / x (l) (x»); 9) + log / xB) (x <«; 9)

• grad0log / xA) xB) (X <«, X <*>; e) — = gradelog / xA) (X «‘>; 9) + gradelog / x <2) (X»>; 0). E6) Вектор справа от E6) независим и равен нулю Имеет матрицу ожидания и ковариации Вы. В этом случае математическое ожидание левого вектора E6) часть равна нулю, а ее ковариационная матрица равна сумме Матрица ковариационных векторов справа, если необходимо Установить. Свойство 1 очевидно. Свойства 2,3 для уменьшения Скалярные параметры и дискретные Вариант. Put Qe (t) =? Pv (x). х: Т (х) = т рассматривать м / aiogPe (X) aiogQe (T (X)) \ «_ elав «J» Напишите ожидаемое значение справа от E7): S Pe (x) Qe (T (x)) P «W1 Qe (,) х т х: Т (х) = т t x: T (x) = t t t

Предположим, что T (x) является достаточной статистикой. По теореме Факторизация (см. Пункт 5 § 15) равенства Pe (x) =? (T (x); c) A (x), E9) Работает каждые 6 в определенном подмножестве 30v. Имеет PV единиц. Для каждого 0 измеренное значение Rv Измерить подмножество ноль 30QXa и вычислить уравнение E9) Выполнено для всех x> 30. Формальная статистика Модель изменилась, но с практической точки зрения 183 Эти изменения не являются значительными. Подводя итог E9), Qe (t) =? (Т; 6) А (х). F0) х: Т (х) = т Замените E9) и F0) слева от E7) и измените их на ноль.

Таким образом, левая сторона E7) / x (c) — / tf «(c). E8) Свойство 2, потому что правая часть E7) не всегда отрицательна Установлен. Людмила Фирмаль

Докажите Свойство 3, рассматривая E8). Свойства 1, 3 Вводить некоторые ограничения, исключая «патологические» Случай. Для краткости предположим, что 8 скаляр, а с не Некоторые интервалы, и, например, <91ogfT! Х) (т; 9) / <Э9F1) / m (X) (b) = 0, быть, т.е. Bb (q log Mx) (T (X); 6) / c> 0) = 0, δ0, Поэтому (см. E3) 6) / c> 6-0, 6e =; e, F2) E ~ b <= — 3 ~ подмножество переменных / Qe вероятность равна единице, Где Qe — распределение статистики T (X). В этом случае Подмножество 0 ‘? 0 это c, отношение F2) удовлетворяется некоторым подмножеством T ‘<=. <= & «, Чья мера Qe равна единству всей паутины ‘. Относится ко всем полотнам по непрерывности F2) W: 4-logMx> (t; e) -0, tedT ‘, Oev, Таким образом, te = ST ‘, ve = 0, F3) Где f (t) 0 независимой плотности. Но это Все 8e0 3 «.U» То есть Qe (^ «‘) = l для всех ve0, доказывая статистическое сходство. Статистика Т (х).

Чтобы доказать обратное свойство 3, используйте Следующее утверждение. Лемма 2 [13, с. 62]. (X, c®, {Po. 9 s 0}) Непрерывная или дискретная модель. Тогда есть счетное подмножество Подмножество 6’E0, любое подмножество X ‘^ X Если все 8e0 ‘Pd (X’) = 0, это уравнение выполнено, Для всех 8e0. Предположим, в это межстрочный интервал, статистика T (x) Информация Е8) так что разница исчезает. Potore Производный от модели требуется 184 jLlogPe (x), J- \ ogQ0 (T (x)), Og0, oQ реклама Более 8 последовательных (определено prx x). Подмножество определено в лемме 2 Подмножество рациональных точек с нуля. E7) С левой стороны, Предположение исчезает, каждые 8ев -l-logPe (x) -iLloBQ0 (T (x)) = <) F4) Подмножество og ^ St? Есть фото майор. В таких ‘<= <%,

Если существует подмножество $, его уравнение (C4) Действителен для всех 0e0’U6 «и хеЯ?, Но также действителен для 0s6’U6» Это верно Re (I? ‘) = 1. F5) Из-за непрерывности уравнение F4) выполняется для всех 8e0, Она? , А лемма 2, равенство F5) это все 8 Поэтому с вероятностью 1 каждые 8ев JLlogPe (x) ^ -logQe (T (x)) — = 0, 0 <= 8 ад Откуда PQ (T ()) фут (), 8 <= е, Где k (x) не зависит от 8. То есть статистика T (x) достаточна. | Логарифмическая база информации Измерение информации не важно, только одно решение Измерение. Расчет статистики удобнее выполнять естественным путем Натуральный логарифм

Смотрите также:

• Решение задач по статистике

Информация по Шеннону	Скалярный параметр
Информация по Кульбаку	Векторный параметр

Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.