Идеальные связи
Идеальными связями называются связи, сумма элементарных работ реакций которых на любых возможных перемещениях точек системы равна нулю. К числу идеальных связей относятся все стационарные геометрические связи без трения.
В том, что сумма работ реакций таких связей равна нулю при всяком возможном перемещении, допускаемом связями, можно убедиться, рассматривая отдельные виды связей.
Так, если связью является гладкая поверхность, то ее реакция, как известно, направлена по нормали к поверхности. Перемещение же, допускаемое такой связью, возможно лишь в касательной плоскости, т. е. всегда будет перпендикулярно к направлению реакции связи, и потому работа этой силы равна нулю.
Если связью служит любой неподвижный шарнир, подшипник или подпятник, то, если пренебречь трением, точка приложения реакции этой связи остается неподвижной при любом перемещении системы и, следовательно, работа реакции равна нулю.
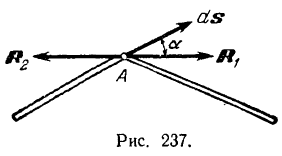
Если связью является подвижный шарнир, соединяющий два тела (рис. 237), то реакция 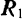 и
и 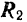 этих тел друг на друга равны по модулю и направлены по одной прямой в противоположные стороны. При любом элементарном перемещении точки приложения (центра
этих тел друг на друга равны по модулю и направлены по одной прямой в противоположные стороны. При любом элементарном перемещении точки приложения (центра 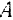 шарнира) реакций этой связи сумма их элементарных работ:
шарнира) реакций этой связи сумма их элементарных работ:
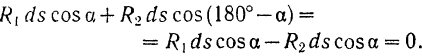
Если связь осуществляется твердым стержнем или работающей на растяжение гибкой нитью (рис. 14 и 13), то приложенные в их концах реакции будут направлены в противоположные стороны вдоль линии, соединяющей точки приложения этих сил, и равны по модулю. Рассуждая так же, как это было сделано в § 105 для неизменяемой системы, мы придем к тому, что сумма работ реакций таких связей при перемещении системы равна нулю.
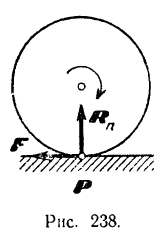
В некоторых случаях идеальными связями могут быть и связи с трением. Например, при качении колеса (рис. 238) по шероховатой поверхности без скольжения на колесо в точке 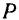 касания колеса действует сила трения
касания колеса действует сила трения 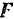 , препятствующая скольжению колеса. Но точка
, препятствующая скольжению колеса. Но точка 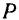 в этом случае является мгновенным центром скоростей колеса и се скорость
в этом случае является мгновенным центром скоростей колеса и се скорость 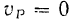 . Отсюда следует, что работа силы
. Отсюда следует, что работа силы 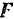 , приложенной в этой точке, равна нулю и данная связь является идеальной.
, приложенной в этой точке, равна нулю и данная связь является идеальной.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

