Идеальные смеси

Идеальные смеси

• Идеальное сочетание Чтобы применить общую формулу в этой главе, вам нужна информация о частичной молекулярной массе (из эксперимента или теории).Во-первых, определите химический потенциал как функцию температуры, давления и состава.Это очень сложная задача, и предстоит еще многое сделать.Однако существует особый класс смесей, позволяющий быстро установить характер зависимости химического потенциала от composition.

To найдите его, определите понятие идеальной смеси по следующим условиям: 1)В — ^ Н .смещение компонента vqr не сопровождается изменением объема. 2)у = 2ин.U) перемешивание r-компонента не сопровождается тепловым эффектом. 3) 5 = ^ / V (У?- kx.in у, энтропия смешивания компонентов совпадает с соответствующим значением идеального газа. из условий Р-1-3 и формулы(6.58) видно, что химический потенциал идеальной смеси характеризуется очень простой зависимостью от состава. [I] (ТТ I, xv …) = [я°я(ТТ Р)+ кт (6.81） Первый срок| я?(7 \ P) является химическим веществом Возможность получения чистого вещества при заданной температуре, давлении, агрегатном состоянии в смеси. Происхождение 2-го члена связано с энтропией смешивания компонентов.

Иногда они представляют собой конденсационную систему, то есть смесь изотопов или Очень похоже molecules.An идеальная смесь, основанная на условиях 1 и 2, характеризуется полной аддитивностью объема и энергии, но, очевидно, невозможно предположить существование такой аддитивности в энтропии, поскольку перемешивание является необратимым процессом.Если компонент полностью смешивается, энтропия увеличивается. А = 5 Б / Д см * * и Г Условие 3、 D5CM = — k в 2 л/, xt. (6.82)） Сначала докажем, что формула (6.82) применима к смеси 2 идеальных gases.It это очень просто.Если газ перед смешиванием занимает объемы Vx и V2 соответственно, объединяя их в один общий объем V1 — | — V/, 2, то каждый газ будет свободно диффундировать в объем, занимаемый другим газом, не взаимодействуя как бы vacuum.As уже видел(гл.2,§ 4, стр. 2) Эта смесь газов приводит к увеличению энтропии AS = Nxk In + V2 + N2kIn V [+ V’2. (6.83）

Сформулированные условия выполняются именно в случае идеального газа, что практически верно для газа в целом. Людмила Фирмаль

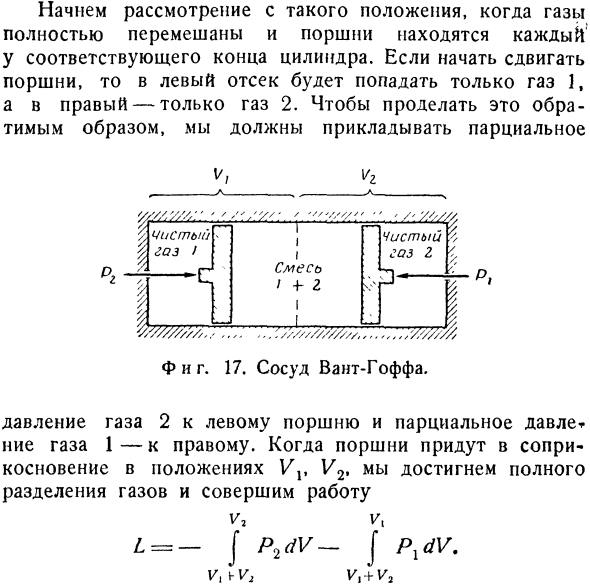
Оба объема газа, естественно, должны быть при одинаковой температуре и давлении, поэтому мы получаем VX’V2 = — xx \ xv. Число= — Nxk в xx-N2k в x2 (6.84） Если вам нужно доказать. Очевидно, что можно расширить доказательства до более чем 3 компонентов;поэтому наше утверждение доказано, но также полезно рассчитать 5 см с учетом обратимого смешивания или разделения 2 gases.To для этого на практике нужно сделать очень тонкие измерения, но для рассмотрения принципа можно воспользоваться мысленным экспериментом, предложенным Вант-Хоффом(1852-1911).Предположим, что оба газа находятся в цилиндрическом сосуде, разделенном на 2 отсека двумя подвижными поршнями (рис.17).Предположим, что поршень слева проходит через газ 1, а поршень справа-через газ 2.

Начните рассматривать с позиции, когда газ тщательно перемешан и поршень находится на соответствующем конце цилиндра, соответственно.Когда поршень начинает двигаться, только газ 1 попадает в левый отсек, и только газ 2 в правый отсек. В. / в. Два В.__— ГПИ ГЛ .. В£ Чистый газ г Я… Смесь I 4-2 Чистого газа я П. С. В / / / / / З///,……,///////// И фигура тоже. 17.Корабль вангов. Давление газа 2 к левому поршню, давление газа 1 к праву. Когда поршень контактирует на положении Vv V2, он достигает полного разъединения газа и завершает работу ва к. L = — [P2dV — [PxdV. VXW2 в> + П2 Минимум этой работы составляет ^ * Арр = н ^ т в y> + + NJtT в + в * .. Конечно, это значение соответствует изменению энтропии, равному-D5SM.

Таким образом, мы видим, что информация, состоящая из пространственного разделения газов, связана с уменьшением энтропии (АС), которую можно получить за счет работы ТАС.Существенным моментом здесь является реальное различие между газами 2 типов 1 и 2.Например, если вы используете природный азот, то он представляет собой смесь из 2 изотопов: N14 (99,62%) и K15(0,38 ° / 0), но если вы не различаете изотопы, вы можете законно считать азот

Как чистый substance.In вопрос, где важно различать изотопы, энтропия азота должна быть дополнена термином, который учитывает смешение изотопов. ДС = — Р(хэто 111 xl15 + х \ a1n х \ а)>(6.85） А если нужно разделить изотопы, то нужно затратить хотя бы тот объем работы, который равен T D5.Используемое значение энтропии зависит от информации о системе и на примере смеси явно видимые компоненты.Независимо от наблюдаемого уровня, если рассматривать энтропию смешивающего компонента как объективное свойство системы, то возникает следующая ситуация: представьте, что разница в атомном весе 2 изотопов изменяется continuously.As пока эта разница существует, как бы мала она ни была, энтропия смешивания компонентов сохраняется постоянной, но если эта разница равна нулю, то энтропия резко изменится в зависимости от величины, определяемой формулой (6.85).

• Эта ситуация известна как парадокс дающего.Конечно, это прекрасно объясняется наличием связи между энтропией и информацией (или между энтропией и отсутствием информации). Потому что распределение определяется перестановками молекул одного вида.Поэтому, согласно принципу Больцмана(см. Главу 2,§ 5)、 5 см = * 1ptb(6-86） И Использование аппроксимации Старлинга \ — NlnN-N、 Получить его снова D5SM = D5id. см = — к£НТ в XI%(6.87） Согласно (6.84). в этом случае не было сделано никаких специальных предположений о состоянии агрегата.Действительно, логарифмический член, характер- Нуль, представляющий собой энтропию идеальной смеси, всегда является основной частью энтропии, даже в случае реальной системы.Однако этот термин соответствует ограничительному случаю полного беспорядка в относительном расположении различных или идентичных молекул.

Однако молекулярные силы, особенно при низких температурах, благоприятствуют образованию специфической, упорядоченной последовательности, в результате чего энтропия смеси несколько ниже энтропии, рассчитанной по формуле (6.87).Точно так же, когда вещество, состоящее из очень разных молекул, смешивается, силы молекул действуют таким образом, что объем и энергия системы меняются, и в идеальной смеси ни одно из трех условий не выполняется.Тем не менее, форма формулы(6.81)имеет вид ji ^ = | d0 — / — x. t(6.88） Так и получилось.： а)почти точно о смеси изотопов、 б)очень точный для смеси веществ, состоящей из одинаковых молекул、 в) для разбавленных растворов он представляет собой соответствующее приближение при расчете химического потенциала растворителя. d) может применяться для расчета химического равновесия по конкретным соображениям.Это будет обсуждаться ниже(см. Главу 7,§ 2).

Давление паров этих смесей представляет собой простую сумму давления паров чистых ингредиентов и соответствующего веса. Р =6,89） Людмила Фирмаль

1.Идеальное давление пара смеси.Типа смесь бромистого этилена — {- бромистого пропилена или тяжелая вода, обычная вода близка к идеальной. Парциальное давление пара каждого компонента пропорционально молярной доле этого компонента в жидкости (закон Генри). чтобы доказать это утверждение, укажите молярную долю компонентов пары в такте、 P. a. s = x’P-xr(6.90） В равновесном состоянии, для каждого компонента (6.91)） То есть химический потенциал должен быть одинаковым для пара и жидкости.Подставляя эти величины в Формулу(6.88), получаем: / Икс： кт в — = — Д | г. (жидкость — > пар). (6.92)） В этом соотношении правая сторона не равна нулю, так как точки H, T отсутствуют на кривой давления пара любого компонента.Но с тех пор AfiJ(7 \ P = P ^ = 0,^ =(6.93） Может быть записан]） С. С. = Дж ДВ] ДП. (6.94） П°.- Предполагая, что в диапазоне P пар рассматривается с достаточной точностью как идеальный газ и игнорирует объем жидкости, Интеграл (6.94) равен Д ^ — Устаканится -^. (6.95）

Новый Этот результат присваивается (6.92), x / .получить jxi-P ^ P, или х / лв = ЛП = ксип°Р(6.96） Соотношение (6.89) и (6.90). Вызов.Состав xx: x2 =2 компонента изотопной смеси£кипит при атмосферном давлении.Если исходить тепло «) Эти расчеты стали в какой-то степени официальными.Это связано с тем, что химический потенциал, как полагают, задается функцией 7 \ P немного за пределами области существования любой фазы.

Испарение одинаково для обоих компонентов; отношение x ‘ {: X2 выводит формулу для пары=|/. Решение.Если уравнять химический потенциал жидкости и пара, то получится аналогичный(6.92). г. Икс kT в—(пар — > жидкость). Правая сторона этого соотношения не равна нулю, так как температура кипения т смеси отличается от температуры кипения чистого вещества. •. 。 • Лс0 = — Л * 0 (Г7)+… = _?- (Г-7)+ Используя формулу давления пара типа (6.30), температура кипения смеси просто Таким образом, сумма соответствующих Весов Терма T = 2、

А у нас есть Я не уверен. В〜= 4Н (Г2-г’) * * 1,1-к = й〜〜 Если вычесть 2-е выражение из первого, то получится желаемый результат. Как и ожидалось, концентрация компонента 1 в паре будет больше или ниже концентрации в жидкой фазе, в зависимости от того, является ли его температура кипения (ТВ) ниже или выше температуры кипения компонента 2. — Техас=)％ Он всегда представляет собой очень малое число, и концентрация в 1 таком шаге будет очень мала.Однако эта концентрация может быть значительно увеличена при использовании многих таких стадий в дистилляционной колонне. Посмотрим, во сколько раз увеличивается концентрация наименее Летучего компонента в остатке, например, компонента 2.При переходе в газовую фазу молекулы dNf-dN, x [dN = dN {- xx dN — \ — N dx { Изотоп 2 в молекуле компонента 1.

Следовательно, изменение молярной фракции отличительное имя. «//Н а / V ИВС =(ХL-ХL) ИК. x [^ xr, так что из предыдущего уравнения = \ С нн％ Или, когда вы интегрируете、 Он всегда представляет собой очень малое число, и концентрация в 1 таком шаге будет очень мала.Однако эта концентрация может быть значительно увеличена при использовании многих таких стадий в дистилляционной колонне. Посмотрим, во сколько раз увеличивается концентрация наименее Летучего компонента в остатке, например, компонента 2.При переходе в газовую фазу молекулы dNf-dN, x [dN = dN {- xx dN — \ — N dx { Изотоп 2 в молекуле компонента 1

.Следовательно, изменение молярной фракции отличительное имя. «//Н а / V ИВС =(ХL-ХL) ИК. x [^ xr, так что из предыдущего уравнения = \ С нн％ Или, когда вы интегрируете、 Поскольку значение Х невелико, для получения значительного обогащения при прямом испарении обычно требуется большое количество материала. Чтобы понять характеристику порядка величины, рассмотрим смешивание воды и тяжелой воды.Разница между температурой кипения тяжелой воды и обычной воды составляет 1,4°С, а теплота испарения близка к 10 500 кал / моль.Это дает 1-ступенчатый коэффициент обогащения. 10500 л <л %= 27373 * м-0,05.

Смотрите также:

Предмет термодинамика

Парциальные молекулярные величины	Общие условия равновесия. устойчивость
Гетерогенные многокомпонентные системы	Неидеальные растворы