


- Идеальная жидкость имеет нулевую вязкость. Наука, изучающая идеальную жидкость, называется теоретической гидродинамикой. Во второй половине 19 века была разработана детальная математическая теория движения идеальной жидкости, и во многих случаях решение уравнений движения было считалось, что воздух и вода имеют низкую вязкость, поэтому они всегда ведут себя как идеальные жидкости, за исключением случаев, когда число Рейнольдса мало. 8. 3. Обтекает цилиндр идеальной жидкостью. Во многих случаях эксперименты показали, что это неверно.
Например, невозможно решить такую практическую задачу, как определение потерь давления при движении жидкости в трубе, используя уравнения теоретической жидкости mechanics. At в то же время, чтобы решить эти проблемы, усилия Эгера-Переса были направлены на создание гидравлики-эмпирической науки, имеющей мало общего с теорией идеальной жидкости. Слияние этих двух ветвей механизма началось только в 1904 году, когда Прандтль выдвинул идею границы layer.
До сих пор считается, что теория идеальной жидкости полностью объясняет движение низковязких жидкостей, удаляющихся от твердых поверхностей. Но вблизи границы есть тонкий слой, в котором происходит практически вязкое трение. Несмотря на небольшую толщину, этот слой оказывает большое влияние на течение вблизи препятствия и силу, с которой жидкость воздействует на это препятствие. Рассмотрим несколько следствий, которые могут привести к тому, что теория идеальной жидкости обтекает объекты простых геометрических форм.8. На рис. 3 показан двумерный горизонтальный поток вокруг цилиндра бесконечной длины.
Поскольку в идеальной жидкости не может быть тангенциального (сдвигового) напряжения, поток разделяется и жидкость обтекает цилиндр и скользит по его поверхности. Расположение линий потока может быть получено путем вычисления так называемого невращательного или потенциального потока. После того, как эта математическая задача решена, уравнение Бернулли может быть использовано для определения распределения давления жидкости. Для идеальной точки линий тока при горизонтальном движении несжимаемой жидкости это уравнение принимает вид: 2-io | P-P0-2- + —потому что рост здесь равен следующему 0(8.7) Точка А, ШОС ноль, получается Р = По4 В 37 — \»Р Е Л) в Г■л т 7-1 9.Степени 8.
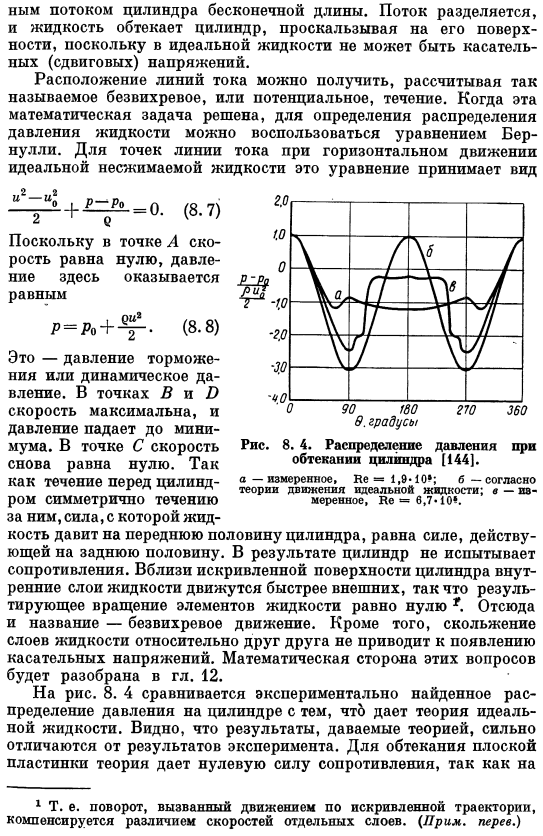
- Распределение давления в потоке вокруг цилиндра[144]. а-измерение, не = 1.9 * 10 *; Б-по теории движения идеальной жидкости. в-меру, он = 6,7 * 10 *. (8.8) Это давление тормоза или динамическое давление. В точке Вий, скорость максимальна, а давление снижается до минимума. В точке C, скорость опять ноль. Потому что поток перед цилиндром симметричен с потоком позади него、 Кость толкает переднюю половину цилиндра, равную силе, действующей на вторую half.
В результате цилиндры не получают сопротивления. Вблизи криволинейной поверхности цилиндра образующийся элемент жидкости оборачивается нулем*, поскольку внутренний слой жидкости движется быстрее, чем внешний*.Отсюда и название-невращательный movement. In кроме того, скольжение текучего слоя относительно друг друга не приводит к появлению напряжения сдвига. Математические аспекты этих вопросов рассматриваются в главе 4. 12. 8. 4. сравните экспериментально найденное распределение давления в цилиндре с тем, которое дает теория идеальной жидкости. Мы видим, что результаты, полученные теорией, сильно отличаются от экспериментальных results.
В случае обрезания плиты теория дает нулевое сопротивление. 1. e. As в результате вращение, вызванное движением по кривой траектории, компенсируется разницей в скорости отдельных слоев. (Примечание, транс) поверхность плиты имеет slipped. In кроме того, нет никаких изменений в давлении и жидкости velocity. As в результате сила сопротивления, наблюдаемая при движении собственно жидкости, обусловлена полностью вязким тангенциальным напряжением, которое связано с изменением скорости течения от нулевой поверхности пластины к невозмущенной U0.As указывается в section.
Как показано на рисунке 12, сопротивление пластины может быть теоретически рассчитано путем интегрирования дифференциальных уравнений движения. Кроме того, сек. вы также можете найти его из известного распределения скорости, используя уравнения баланса импульса, как показано на рис.
| Ламинарное течение в круглой трубе | Идеальная жидкость |
| Потоки импульса, количества движения, массы и энергии | Пограничный слой |
