Оглавление:





Характер напряжений в балке. Изгибающий момент и поперечная сила
- Характер напряжения пучка. Изгибающий момент и поперечная сила. Выбор расчетной схемы решает первую часть задачи о силе, действующей на балку. Это будет следующим шагом в решении проблемы изгиба. Возьмем Луч в качестве объекта для рассуждения (рис. 151 шарнирные концы) И расчет реакции поддержки вычисления луча-определение внешнего напряжения в разделе, который нужно найти Семьдесят семь / 2^ Но — / / 1 Один. Р2 / Загружен мощность РІ, Р * Р3. Реакция в данной системе нагрузок равна нулю, а реакции A и B определяются из уравнения момента.
При расчете напряжения необходимо найти опасную часть балки, через которую передается максимальное напряжение. Для этого необходимо получить выражение, в котором можно рассчитать напряжения любого сечения (например, наклон сечения 2–2). Затем вычислите напряжение в сечении, параллельном оси, а затем в любом сечении. Возьмите сечение, перпендикулярное центру тяжести O и оси TP на расстоянии x от левой опорной кромки. Чтобы рассчитать напряжение в этом сечении, опустите часть балки и замените ее действие на оставшееся требуемое напряжение.
Для простоты расчетов необходимо оставлять части балки с меньшим Людмила Фирмаль
усилием.§ 70] характер напряжений в балке 227 / / Фигура. Сто пятьдесят два.7/7% X+1 К — — — Х — — — й Г В — ^(5 Левая часть балки(рис. 152) действует напряжение в каждой точке сечения TP, которое может быть представлено компонентой: нормалью a и касательной T. эти напряжения образуют систему внешних сил a и внешних сил и сил в пространстве, которые вместе могут составлять шесть уравнений равновесия. Если вы попытаетесь
вывести напряжение a и напряжение t из этих уравнений, система внешних сил, приложенных к возможным частям, не будет одинаковой, поэтому для каждого участка (например, для участка между левой силой P2 и P3, где x изменяется) вместо двух применяются три силы. Для получения А и Т общих формул, подходящих для любого значения Х, следует отметить, что система внешних сил, действующих на левую часть, всегда должна быть
- в однородном стандартном виде. Поскольку эта система состоит из сил, находящихся в одной плоскости, их всегда можно заменить парой сил, центром редукции, и силой, приложенной в определенный момент времени, что дает возможность всегда приводить в систему силы, действующие непосредственно на левую часть луча, достаточно простой и в то же время однородный вид. Центроид рассматриваемого сечения обычно принимается за центр редукции, что значительно упрощает формулы для вычисления О и т, как мы видим. В рассматриваемой левой части пучка мы заменяем силу A и эквивалентную систему и применяем систему реакции A
в этой точке и эти две силы концентрируются в точке B, пересекаются дважды), применяем в точке O и к паре сил (один раз пересекаются) X и. Момент этой пары-ах. Точно так же, как мы это делаем, мы складываем силы и добавляем к ним все дважды пересеченные силы, приложенные к точке О, и все пары моментов, состоящие из раз пересеченных сил, а затем учитываем положительное направление силы и положительное направление направления по часовой стрелке. Точно так же, доведя их до точки двух сил вверх и ’ФЛ’ О(рис. 153). Спускаться. Зет 8 * 228 испытание на прочность при изгибе[глава XII В
результате сложения вместо силы A получаем Людмила Фирмаль
силу Q, приложенную к центру тяжести сечения, а значения m и Q равны m-A x-RG(x-a j, Q=A-P T. Изгибающий момент также можно считать моментом системы сил, которая в данном сечении заменяет действие отброшенной части балки на остальные. Изгибающий момент M равен сумме моментов всех внешних сил, приложенных к рассматриваемой части балки, относительно центроида сечения. Сила Q, которая стремится переместить левую часть балки против отброшенной, называется поперечной (или режущей) силой в этом сечении. Боковая сила Q может также рассматриваться как проекция на поверхность поперечного сечения системы равнодействующих сил, в данном сечении, для замены действия отброшенной части
балки на остальную часть части. Боковая сила Q равна сумме проекций всех внешних сил, приложенных к левой части балки, перпендикулярной ее оси. Таким образом, м и Q заменили систему внешних сил, приложенных к рассматриваемой части балки, и переданных через проводимую часть со стороны отбрасываемой части балки. Будьте внимательны, под действием силы Луча только перпендикулярно его оси можно говорить о боковой силе., О полной силе как алгебре, подходящей для левой части балки Это неудивительно, поскольку они представляют собой системы стандартной формы, заменяющие системы А и Р, применяемые к рассматриваемой части балки. Эти определения отвечают на вопрос о том, как вычислить M и Q из заданной внешней силы. Для вычисления M и Q в приведенном выше примере мы рассмотрели левую часть балки, но во многих случаях удобнее рассмотреть правую часть в расчете и отбросить левую часть. Установите связь между
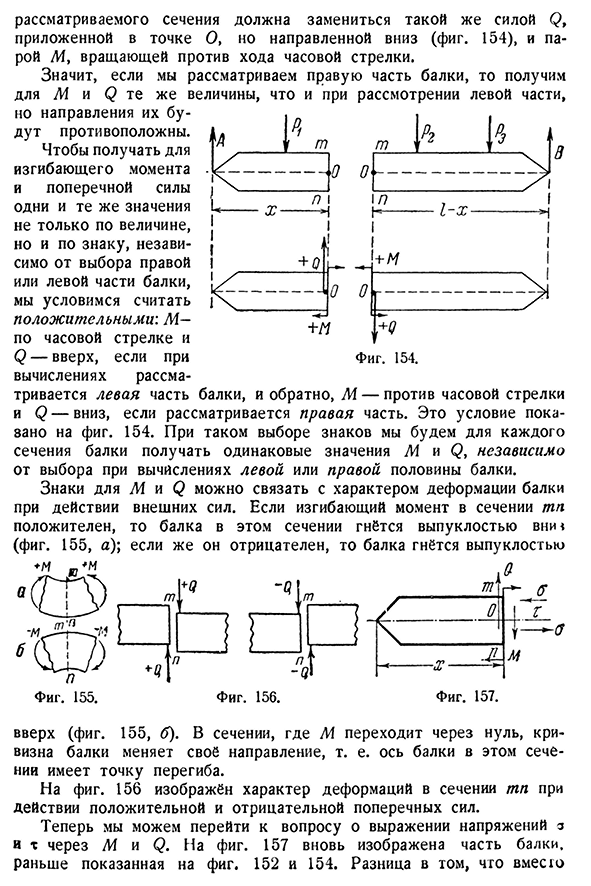
значениями M и Q для левой и правой частей луча. Как использовать 154 система внешних сил а действует на часть балки с левой стороны правого участка ТП-системы Р3 и В. Потому что весь Луч в целом(рис. 154) находится в равновесии, то система сил A и Px должна уравновесить систему сил P RZ и B. первая система приложена к точке O В точке О рассматриваемого участка должна быть заменена та же сила Q, приложенная, но вниз(рис. 154), против вращения против часовой стрелки. Итак, если принять во внимание правую часть луча, то получим те же значения для M и Q, как если бы мы приняли во внимание левую часть, но в противоположном
направлении. Чтобы получить изгибающий момент и силу сдвига, чтобы получить одинаковое значение не только по величине, но и по знаку, независимо от правого или левого выбора балки, мы показываем положительное это состояние на рисунке. 154. Этот выбор знака дает одинаковые значения M и Q для каждого участка балки, независимо от выбора при расчете левой или правой половины балки. Признаки M и Q могут быть связаны с характером деформации балки под действием внешних сил. Если изгибающий момент участка TP положительный, то балка этого участка изгибается центральной выпуклой частью(рис. 155, а); если отрицательный, то луч выпукл и изогнут Вверх (рис. 155, б). В интервале, в котором M проходит через ноль, кривизна луча меняет свое направление. Способ применения 156 указывает на характер
деформации в поперечном сечении ТП под действием положительных и отрицательных боковых сил. Здесь мы можем перейти к задаче выражения напряжений a и t через M и Q. 157 снова показывает некоторые из балок, ранее показанных на рисунке. 152 и 154. Разница заключается в том, что испытание на прочность hho230flexural [CH. ДВЕНАДЦАТЫЙ Напряжение О и напряжение т, которые заменяют действие правой отброшенной части, должны уравновесить эту систему внешних сил. Нормальное напряжение A не способно уравновесить силу Q. но они могут образовать пару, уравновешивающую изгибающий момент 7I, так как L1 направлена параллельно плоскости симметрии балки, в которой она присутствует. Таким образом, нормальное напряжение a зависит только от M, с другой стороны, а тангенциальное напряжение
t не способно уравновесить пару L4, лежит на плоскости TP и не соответствует рабочей поверхности изгибающего момента. Таким образом, мы приходим к выводу: боковая сила Q уравновешивается только тангенциальной силой, сумма которой должна быть равна силе Q.: (12.1) (12.2) Выходы формул (12.1) и(12.2) достаточно произвести только один раз для любого участка балки. В дальнейшем эти формулы могут быть использованы в любом разделе, но вам нужно только найти значения M и q. Чем больше напряжения o и t, тем больше L1 и Q; поскольку нам нужно найти максимальное значение этих напряжений для проверки прочности материала, у нас есть график, показывающий, как значения L4 и Q различных участков балки изменяются в соответствии с так называемой диаграммой изгибающего момента и боковой силы, т. е.,
Смотрите также:

