Оглавление:


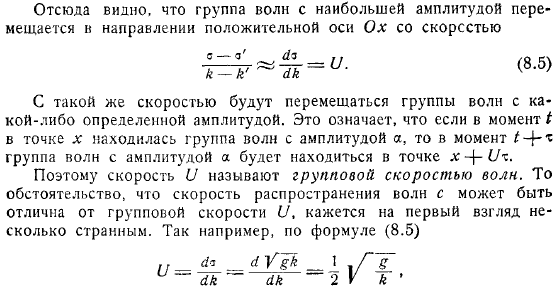





Групповая скорость
До сих пор мы рассматривали серию последовательных волновых движений, которые полностью идентичны среди них. Если рассматривать группу волн разной длины волны, то явление усложняется. Мне показалось гидромеханика очень полезным ввести понятие группы.
Как мы увидим позже, групповая скорость является важным динамическим свойством волнового процесса, поскольку она определяет скорость передачи энергии волнами. Проясните это понятие в простой. Другими словами к установившемуся движению , добавьте потенциала формы с различными потенциалами формы.
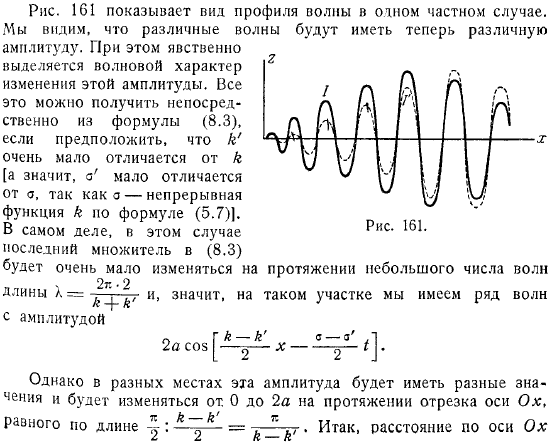
- Уравнение, определяющее тип свободной поверхности, в этом случае выглядит следующим образом. Указывает тип профиля сигнала для конкретного случая.
- Разные волны будут иметь разные. В этом случае волновые характеристики изменения этой амплитуды четко различаются.
Это можно получить непосредственно из выражения, предполагая, что оно почти не изменяется от. Людмила Фирмаль
Дело в том, что в данном случае последний фактор практически не меняется. Следовательно. На нескольких волнах такого участка мы имеем несколько волн.
Однако в зависимости от местоположения эта амплитуда имеет разные значения и изменяется в зависимости от длины оси. Равны по длине. Следовательно, расстояние вдоль оси между группами по смежных волны с максимальной амплитудой равны.
- Рассматриваемый случай демонстрирует много особенностей по сравнению с предыдущими. Во-первых, форма профиля волны всегда изменяется непрерывно.
- Это видно, например, из Формулы. Из форм волны видно, что она получается путем сложения различных косинусных волн, движущихся с разной скоростью и таким образом смещающихся друг к другу.
Далее отметим примечательный. Известно, что только форма поверхности движется в волновом движении. Возьмите конкретную волну и отслеживать его. Мы видели, что амплитуда этой волны изменяется очень медленно, а сама волна движется со скоростью в сторону положительной оси.
Далее рассмотрим всю группу волн, имеющих наибольшую амплитуду. Людмила Фирмаль
Эта максимальная амплитуда берется для следующей точки оси. Это указывает на то, что группа воды с максимальной амплитудой движется со скоростью в направлении положительной оси с той же скоростью движется группа волн с определенной амплитудой.
Если это в какой-то момент, если бы существовала группа волн амплитуды а, то в этот момент группа волн амплитуды а была бы точкой. Поэтому и скорость называется. Тот факт, что скорость распространения волны может отличаться от групповой скорости, на первый взгляд кажется немного странным.
Например, по формуле это значит другими словами, скорость распространения групповой волны в раза превышает скорость распространения отдельной волны. Это, например, указывает на то, что когда определенная волна входит в положение распространения на расстоянии волны, амплитуда рассматриваемой волны увеличивается, потому что вся группа перемещается на расстояние.
В дальнейшем случай плоской задачи и амплитуда рассматриваемой волны будет продолжать увеличиваться до тех пор, пока амплитуда не станет максимальной, а затем амплитуда будет уменьшаться, и так далее. Таким образом, мы видим, что при распространении определенной волны эта волна движется в направлении положительной оси группы волн. Из этого становится ясно, что скорость распространения истинной волны может отличаться от скорости движения группы.
Эти разности скоростей показывают, как быстро волны распространяются относительно группы волн. Будьте осторожны с ним. Разница между скоростью распространения волны и скоростью распространения волны возникает только тогда, когда скорость распространения волны зависит от их.
В данном случае речь пойдет о рассеянии волн. Групповая скорость волны определяется уравнением, из которого мы получаем критическое уравнение для групповой скорости, обозначенной Рэлеем. Этому выражению можно придать простое геометрическое значение.
Просто нарисуйте график с точками в функции и с координатами, которые рисуют касательную. Последнее уравнение выглядит так: мы видим, что существует отрезок, отрезанный этой касательной на оси. Мы также находим форму орбиты частицы в рассматриваемом движении.
Потому что последний можно считать композитом из движений формы. Движение каждой частицы можно представить следующим образом. Опишите круг с радиусом около точки. Пусть эта точка является центром новой окружности с радиусом вдоль этой окружности, частицы движутся периодически.
Так называемая удлиненная или укороченная эпициклоида действует как след частицы.Частица приблизительно представляет собой круг разных радиусов и имеет периодичности. С одной стороны, существует период круга, а с другой стороны, существует период изменения радиуса круга.
Это соответствует скорости распространения отдельных волн и наличию групповых скоростей волн. Для простоты при рассмотрении задачи о групповой скорости мы ограничились сложением волн с одинаковой амплитудой и разными длинами волн. Если добавить много волн примерно одинаковой длины волны, то расчет будет более сложным, но суть задачи останется неизменной.

