Группировки элементов конечного множества.

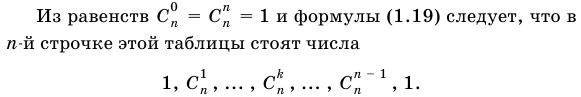
Группировки элементов конечного множества.

Группировки элементов конечного множества. Если задано конечное множество, то удобно составить несколько групп, удовлетворяющих своим элементам или другим условиям, и исследовать их свойства, например, чтобы выяснить, сколько таких групп может быть составлено. Рассмотрим группу элементов, называемых аранжировками, перестановками и комбинациями. дано множество из n элементов、 х1, х2,…xn.」 ） И некоторое положительное целое число V является fixed. In Определение 5.Группа элементов, каждая из которых состоит из V элементов и отличается друг от друга самими элементами или их порядком, называется массивом из V n элементов. Например, группа{1、2}、{2、1}、{1、3}、{3、1}、{2、3}、{3、2}Составьте любую композицию из 3 натуральных чисел 1, 2, 3.2 из них. Количество всех механизмов из n элементов по элементов V ПСР, n = 1, 2,…V = 1, 2,…обозначается через n. Для леммы V p、 ПСР + 1 = ПСР(n-V). (1.9).

В остальной части этого раздела подразумевается, что элемент всегда является элементом (1.8), если, конечно, не указаны другие элементы. Людмила Фирмаль

• Все размеры в этом путе V + 1 элемент и только 1 time. So … ПСР (n-V)= An + 1). 29 декабря Теорема L. существует формула места (1.10) т. е. формула (1.10) справедлива. Теорема доказана. Очевидно, что в соответствии с математической индукцией достаточно было проверить правильность уравнения (1.11) и указать, что уравнение (1.13) следует за уравнением (1.10).Определение 6.(n = 1, 2,…это не так. Например, группа{1、2、3}、{1、3、2}、{2、1、3}、{2、3、1}、{3、1、2}и{3, 2, 1}образуют всевозможные перестановки из первых 3 натуральных чисел 1, 2, 3. число всех перестановок n элементов обозначается через Pn. Т Е О Р Е М А 2.Уравнение Pn = 1 * 2•…существует * p. Это сразу следует из уравнения k = n (1.10).Продукт 1 * 2•…•Н! На это указывает (читай.»Факторный.)»Принятые обозначения РП = N! (1.14） Для удобства укажите P0 = 0! = 1. Тридцать Определение 7.Группа, каждая из которых состоит из V элементов и по крайней мере 1 элемент отличается, называется комбинацией.

• Например, группа{1、2}、{1、3}и{2, 3}образуют все комбинации из 2 натуральных чисел 1, 2 и 3 соответственно. число всех комбинаций из n элементов и V элементов Это обозначено SKP, соответственно. Теорема 3.Есть один чиновник. Доказательство. Если вы хотите создать все возможные перестановки этого элемента со всеми комбинациями n элементов вдоль V (все Cn) (количество таких перестановок равно Pk), вы можете получить выравнивание из n элементов вдоль V и, таким образом, получить все размещения из n элементов вдоль V и многое другое once. So … СК Р _ ЛК СПРК ЛВ、 Отсюда следует выражение (1.15).Формула (1.16)（1.10）、（1.14）、（1.15） его получают из В числителе и знаменателе правой части формулы (1.16) (n-V)!При умножении получается формула (1.17). Теорема 4.Есть такой чиновник Skp_Spn-k, V_0, 1, 2,…Н (1.18)） это хорошая вещь. 04еТ.. Вот, cn _ 1. Доказательство. Выражение (1.18) легко получить непосредственно из определения комбинации. При выборе группы (комбинации) из n элементов, состоящей из V элементов, группа (Комбинация) из n-V элементов остается, и таким образом вы получаете все комбинации n элементов из n-V элементов и 1 time. So, число комбинаций n элементов относительно k, то есть SKP, будет равно числу комбинаций n элементов относительно n-k, то есть SP K. Уравнение (1.18) следует непосредственно за уравнением(1.17). Теорема 5.

Группа, состоящая из одного и того же числа элементов и отличающаяся друг от друга только порядком следования элементов, называется перестановкой. Людмила Фирмаль

• Количество последующих комбинаций Этот входной элемент является тем же самым, что и совместное предприятие (потому что если вы отбросите каждую такую комбинацию, вы получите комбинацию всех видов n элементов для k элементов только один раз), и если вы этого не сделаете, вы не сможете использовать ту же комбинацию. Число комбинаций, которых он не содержит, равно SPT1 (для формирования комбинаций всех видов K T 1 элементов из оставшихся n элементов).Это доказывает формула (1.19). Замечание. Число SP можно найти, используя следующую треугольную таблицу, называемую треугольником Паскаля 1.Здесь первое и последнее число всех строк равно 1, начиная с 3-й строки, и каждое число, отличное от первого и последнего, получается путем сложения 2 чисел, ближайших к предыдущей строке. Б. Паскаль (1623-1662) французский математик. Из уравнения c°n = Cn = 1 и уравнения (1.19).

Смотрите также:

Предмет математический анализ

Функции.	Логические символы.
Конечные множества и натуральные числа. Последовательности.	Свойства действительных чисел.