Оглавление:







Гравитационный коллапс сферического тела
- Гравитационный коллапс сферического тела. Для метрики Шварцшильда (100,14) гу исчезает, И gn — r = rg (на сфере Шварцшильда), это бесконечно. Эта ситуация приводит к выводу, что существует метрика пространства-времени, а затем К выводу о невозможности существования тела с «радиусом» Меньше радиуса гравитации (для данной массы).
В эксплуатации Однако этот вывод не верен. ми Это определитель Поскольку g = -r4 sin2 не имеет специфичности при r = rg, Условие g <0 (82,3) не нарушается. Будет ли это на самом деле увидеть иметь дело только с невозможностью реализации г < Строгая справочная система. Разъяснить суть пространства-времени Метрики переменных в этой области выполняют следующие преобразования
новая система Координаты также синхронизированы Людмила Фирмаль
Вид профиля 1) cr = ± c t ± [/ (r) φ ~, R = ct + [——- dr (102.1) J l-Tg / r J (l-r g / r) f (r) тогда ds2 = ~~~ ^ ~ (c2dr2-f 2dR2) -r2 (d02 + sin2 6 dip2). Выбирая f (r), мы исключаем специфичность r = rg. f (rg) = 1. f (r) = y / rg / r), (gTT = 1). Первый выбор Для ясности верхний символ (1 0 2 .1), 2 ^ 2 ZgU 2 ’ E-c m = [± -1 ^ ± = [^ d r = J {1-rg / r) f J rg А л и 2/3 G = (R-й) ‘> Y 3 (102,2)
Я (Интегральная постоянная в соответствии с постоянной времени Измените m и установите его на ноль). Интервал элемента: ds2 = c2dr2 ————— \ {R ~ CT) ^ r2 / s (d62 + sin2 6d (p2). Ј <* ->] ■ L2 (102.3) В этих координатах сферические объекты Шварцшильда 3 (Это соответствует уравнению — (R-й) = RG) Это верно Координата R является пространственной всюду, и т Временный. Метрика (102.3) является переходной.
- Как и синхронная система отсчета, ее временная шкала является геодезической. Другими словами, отдых относительно Система отсчета «тестирующих» частиц — это частицы свободно Переезд в это поле. Указанное значение r соответствует мировой линии R-st =. = const (диагональная прямая на рис. 20).
Мировые линии частиц, которые являются стационарными относительно системы отсчета, показаны на этом рисунке в виде вертикальных линий. Конечно разнесенные частицы, которые движутся вдоль них Подходящее время «падает» на центр поля (r = 0). Это истинная особая точка метрики.
Два знака соответствуют двум границам светового Людмила Фирмаль
Рассмотрим распространение радиально-оптических сигналов Уравнение промысла ds2 = 0 (если 0, <p = const) дает продукцию Ноа др / д.р. вдоль луча: «конуса» сверху Ной в указанных мировых точках. Когда r> rg (точка А на рисунке 20)
Наклон этих границ равен \ cdr / dR \ <1, поэтому линия r = const Действия и сигналы распространяются здесь Добраться до центра за ограниченное время t. Аналогично, выбрав (1 0 2 .1) в преобразовании Низкие знаки, мы получаем «расширенную» систему Кадры с метриками, отличными от (102.3) из-за изменений (102,4) T Рисунок 20 (Cdr / dR = l вдоль него) вписывается в конус.
В области r <r g (точка а ‘) \ cdr / dR \> 1 r = const — мировые линии, которые не двигаются (относительно Центр поля частиц) — вне конуса. Обе границы Пересечь линию r = 0 на конечном расстоянии Подойдите к ней вертикально. Потому что нет причинно-следственной связи Связанное событие не может быть в мире Вне светового конуса область r <rg Частицы не застревают.
Все символы до т. Это Остальное все еще невозможно (с областью r <rg), Все сигналы уходят из центра. Приведенные выше результаты могут быть применены к следующим вопросам: О массовом теле в общей теории относительности.
Изучение состояния релятивистского равновесия сферы Показывает, что тело достаточно велико для тела Возможно, система не находится в равновесном статическом состоянии. (См. «Статистическая физика», часть 1, §109). по-видимому Тело должно сокращаться до бесконечности (так называемый гравий Национальный крах) х).
В системе, которая бесконечно связана с телом Галилеи Контрольный (метрический (100,14)) радиус центрального тела равен меньше чем рг. Это означает, что согласно часам t удаленного наблюдателя радиус сокращающегося тела является только асимптотическим. t- »oo имеет тенденцию иметь гравитационный радиус.
Легко найти Окончательный закон этого приближения. Все частицы на поверхности сокращающегося тела Время полной массы в гравитационном поле постоянной массы t Тело По мере того как сила тяжести становится очень большой. Плотность (и давление) тела остается конечной.
до Игнорируя силу давления, основанную на этом, мы уменьшим Делим зависимость радиуса тела от времени, чтобы рассмотреть Свободное падение пробных частиц в поле массы m. Учитывая зависимость r (t) для попадания в поле Шварцшильда Интеграл (101.4) и для чисто радиального движения Момент М = 0. Так что, если падение начинается с «расстояния» ро
В какой-то момент из центра нулевой скорости Энергия частицы §§ = t c2 y / 1-rg / ro и время достижения t Судя о ее «расстоянии» _____ й c (t —10) = 1/1 — f ————- ^ (102-5) V r ° J (! -Rs / r) V rg / r-rs / rо G Этот интеграл расходится как r- »rg as-rg In (r-rg). Отсюда Асимптотический закон приближения от r до rg: r-rg = const • e ~ ct / Tg. (1 0 2 .6)
Поэтому последний этап аппроксимации рушится Происходит экспоненциально с телом против радиуса гравитации Основной закон с очень коротким характерным временем составляет ~ г / с. Скорость сжатия, наблюдаемая снаружи, является асимптотической, Стремится к нулю, а скорость падающей частицы v равна Наоборот, мое время увеличивается, и я стремлюсь к скорости Света.
Фактически, согласно определению (88.10): v 2 = / y / = gH dr \ 2 V y / g ^ dt J Если вы получаете gn и goo из (100.14) и получаете dr / dt из (102.5), 1-4 = (102,7) C 1-Tg / Tq Приближается к радиусу гравитации и бесконечно необходим Ночь времени под наблюдением далёкого наблюдателя, Только ограниченный интервал подходящего времени Опорная рамка).
Это уже ясно из вышесказанного. Общий анализ, но это можно увидеть непосредственно Вычисляя подходящее время t как инвариантное целое число Gurara [a [Γ2 dt * — | V2 CT = / ds = / c g o o ^ j + g n J dr. Если вы получите dr / dt из (102.5), вы знаете правильное время падения Переместиться из точки в g. Перейти m-m ° = 1с-1 & -rn) 112 г Этот интеграл сходится при r-> rg.
Достигнут гравитации (в нужное время) Диус, тело продолжает сжиматься и все такое Столица достигла своего центра в последний час. момент Падение вещества в центр каждой части Облачная особенность метрик пространства-времени. все Однако процесс сжатия тела под сферой Шварцшильда Наблюдайте из внешней системы отсчета. Момент, чтобы пройти Поверхность этой сферы соответствует времени t = os.
Вы можете Скажем, весь процесс распада под сферой Шварцшильда Это происходит так, как будто дистанция «вне времени бесконечности» Наблюдатель является крайним примером относительности хода времени. Конечно, в этом рисунке нет логического противоречия.
Нет, следуй полностью Свойства справочной системы контракта: из-под этой системы Сигнал от сферы Шварцшильда отсутствует. частица Или луч может пройти эту сферу только в одном направлении (в пределах соответствующей системы отсчета), то есть внутрь и только один раз. Пройдя туда, вы никогда не сможете вернуться снова.
Поверхность такого «одностороннего клапана» Он существует. Сжатие в гравий для внешнего наблюдателя Радиус станции сопровождается «самозакрывающимся» корпусом. Время распространения сигнала, передаваемого телом, составляет До бесконечности. Фактически для оптических сигналов ds2 = O А для системы Шварцшильда cdt = dr / (1-rg / r) \ time
Распространение от r до r> r определяется интегрированием Перейти cAt = [-dr = tq-r + rg In—, (102,9) Дивергенция как r-rg (например, интеграл (102.5)). Соответствующие временные интервалы на поверхности вишневого тела Будет удалено на неопределенный срок за интервал времени t На наблюдателей V ^ O = Y 1-7; r- »r * g, а значит и все процессы, относящиеся к организму «Заморозить» внешнего наблюдателя.
Спектральная частота Линия, излучаемая телом и воспринимаемая дистанционно Наблюдатели также уменьшают этот эффект гра Не только важное красное смещение, но и эффект Доплера Движение источника падает по поверхности к центру Болл.
Если радиус шара уже близок к rg (отсюда скорость Падение уже близко к скорости света), этот эффект уменьшен частота V 1-V2 / s2 ^ 1 / -, _ 1 + v / c ~ 2 В с2 Времена. Наблюдаемая частота под влиянием обоих эффектов В результате исчезают как r- »rg согласно закону ω = const ^ 1 -— Y (1 0 2 .1 0)
Поэтому с точки зрения дальнего наблюдателя, гра Крах жизненных сил приводит к «заморозке» Тело не отправлено в окружающее пространство Обмен сигналами с внешним миром, 100 Гравитационное поле. Такая сущность называется Черная дыра или коллапс. 14 * В заключение я сделаю еще одно утверждение о методологии. Трактор.
Неактивен в среднем поле в пустоте Бесконечно далекое общество «Система внешних наблюдателей» полный: некуда двигать мировую линию частиц Внутри сферы Шварцшильда. Метрика (102,3) применяется Эта система также используется внутри сферы Шварцшильда.
Ссылка в некотором смысле не полная. Конечно, пожалуйста, подумайте В этой системе частицы, которые движутся радиально По направлению от центра. t worldline- »oo исчезает Бесконечно и асимптотически как r- »os Подход r = rg. Движение сферы Шварцшильда К центру. Между тем, продвижение частиц r = rg в любую точку r> rg Ный интервал собственного времени.
В мое время Также поэтому частицы должны приближаться к Шварцшильду Сфера изнутри, прежде чем начать двигаться снаружи. Но эта часть История частиц не охватывается этой системой отсчета1). Однако это несовершенство Формальная экспертиза созданных полевых метрик Вторая точка масс.
Например, в реальных физических проблемах Обширные разрушения тела, недостатки не проявляются: Подробнее Результаты, полученные путем объединения метрик (102,3) с решениями Внутренняя часть вещества, конечно, завершена и описывает Полная история всех возможных движений частиц (мировые линии Частицы движутся в направлении от центра в области r> rg, Конечно, начинается с поверхности мяча, прежде чем Сжатие в сфере Шварцшильда).
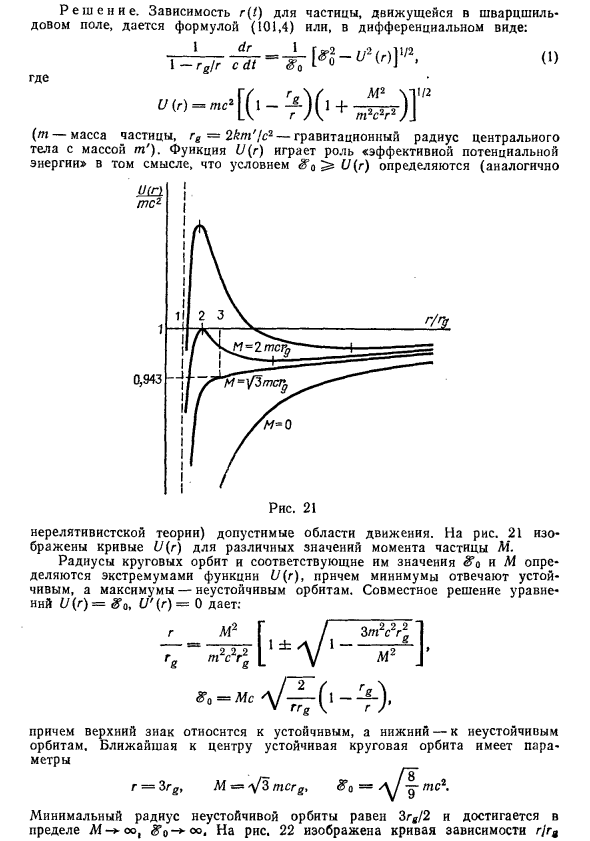
Задача 1. Найти радиус круговой орбиты для частицы в свернутом поле {С.А. Каплан, 1949). Решения. Зависимость частиц, движущихся в Шварцшилле r (t) Поле задается формулой (101.4). Или в дифференциальной форме, (M — масса частицы, rg = 2kt / s — радиус центра тяжести Масса т) кузова. Функция TJ (r) играет роль «эффективного потенциала»
«Энергия» означает, что условие S’O ^ U (r) определяет допустимую область движения (как в нерелятивистской теории). 21 лист Кривая U (r) показана для различных значений момента частицы M. Радиус круговой орбиты и соответствующие значения So и M
Определяется предельное значение функции U (r), минимальное значение Стабильная, максимально нестабильная орбита. Совместное решение Уравнение TJ (r) =, поэтому U ‘(r) = 0 M2 г / 3м2c2rl и ^ / 2 / ge \ -5-5- 5- 1 ± 4/1 ——- 5-S-, 4> = M cJ— (л m c r2 L y M J y rrg V g / Кроме того, символ выше Чистая и донная нестабильность Bit. Стабильность ближе всего к центру Круговые орбиты имеют параметры r = 3 rg, M = 1/31 = a / 879 »
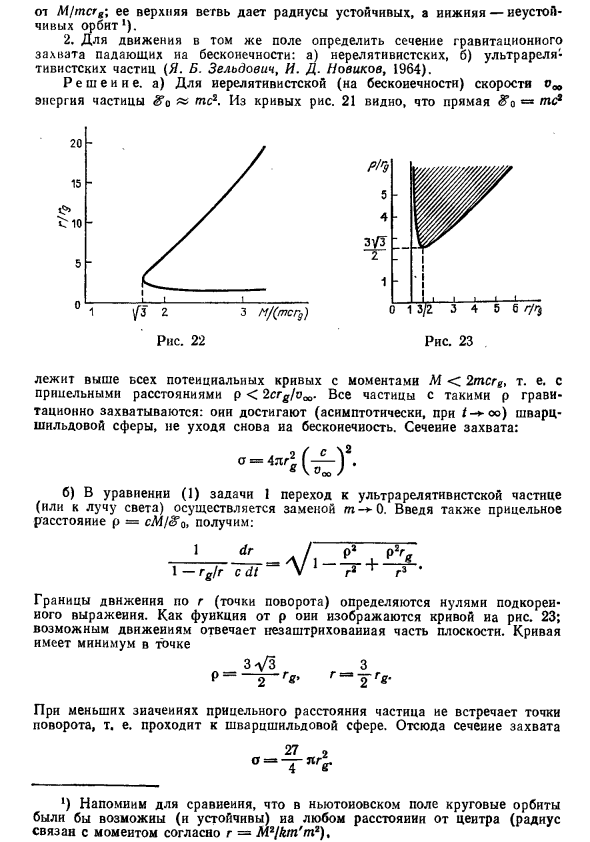
Минимальный радиус нестабильной работы Бит равен 3rg / 2 и достигает в определенных пределах М — >> оо, так оо. Рисунок 22 показан кривая r / rg против M / (m crg); она Верхняя ветвь имеет устойчивый радиус 2. Для движения в том же поле определите сечение силы тяжести Бесконечный захват: а) нерелятивистский, б) супер-релевантный Тивистские частицы (Я. Б. Зельдович, И. Д. Новиков, 1964). Решения. а)
Нерелятивистская (бесконечная) скорость r? оо, энергия Статья «mc2. Рисунок 21 из кривой на рисунке показывает, что линия So = mc2 выше Все потенциальные кривые с моментом М <2 мкгр, т.е. затронуты Расстояние р <2кг / ух. Все частицы с таким p-гравитационным захватом Исчезают: они достигают Шварцшильда (асимптотически при t-oo) Сфера, не возвращаясь к бесконечности.
Захват раздел: к 2 4 т г т \ (-) б) Переход к суперрелятивистским частицам в уравнении 1 задачи 1 (Или лучу) выполняется заменой m-0.0. Расстояние р = см / кв. PhD + Г 1-й курс Граница движения вдоль g (точка поворота) определяется Радикальное выражение делится на ноль. как функции р, они представлены кривыми выше Рисунок 23;
Возможные движения встречаются Заштрихованная часть самолета. Кривая Минимум в баллах 3 ^ 3 3 р = —— 7В, Т = -7В. 2 2 Небольшое расстояние удара Частицы не встречают поворотного момента, то есть переходят к Шварцшильду Сфера. Так что раздел захвата 27 2
Смотрите также:
| Центрально-симметричное гравитационное поле | Гравитационный коллапс пылевидной сферы |
| Движение в центрально-симметричном гравитационном поле | Гравитационный коллапс несферических и вращающихся тел |

