Оглавление:






Гравитационное течение пленки жидкости
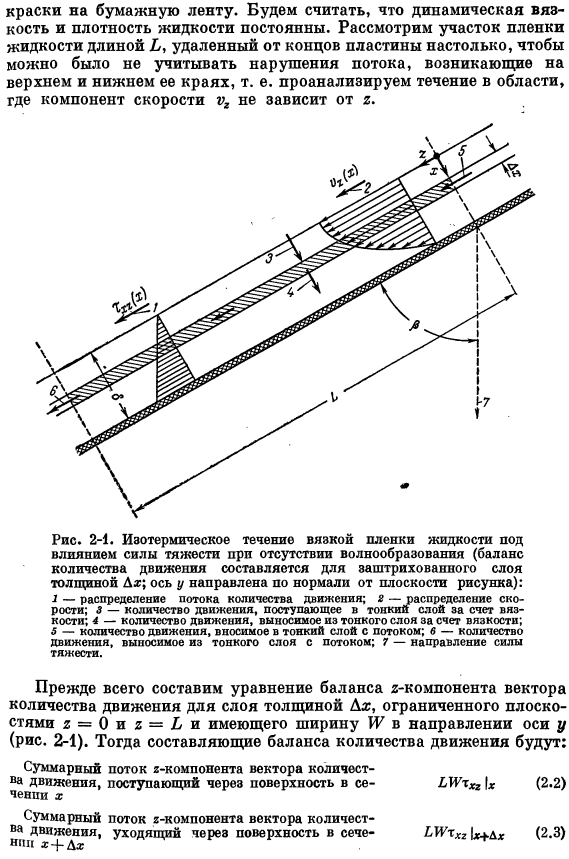
- В качестве первого примера рассмотрим течение жидкости вдоль наклонной плоской поверхности. Исследование такого тонкого слоя жидкости проводится при работе колонн с орошаемыми стенками в процессе испарения и в процессе поглощения гаэов, а также краска на бумаге tape. It предполагается, что динамическая вязкость и плотность жидкости постоянны. Рассмотрим часть жидкой пленки длиной b, которая находится далеко от края plate. It не удалось учесть турбулентность потока, возникающую на верхней и нижней кромках.
То есть мы анализируем поток в этом районе Сначала составим уравнение для баланса 2 компонент вектора импульса слоя толщиной Dx, ограниченного плоскостями a = 0 и 2 = Li с шириной и ’в направлении оси y(рис. 2-1).Тогда элемент баланса импульса будет: Количественный Хит » / x (2.2) Суммарный поток из 2 составляющих вектора импульса, проходящего через поверхность (И ’ дя>), риг 1м (У Диа ^ ПМ.、 (2.5) (2.Е Обратите внимание на термин » входящие…..- он сказал, что собирается уходить. Следующее[например, см. формулу (2.28)〜(2.34)] относится к положительному направлению осей x и 2(в описанной задаче эти направления совпадают с направлением передачи импульса): Index / x.
Вычислите коэффициенты локального теплообмена для турбулентного пограничного слоя вдоль плоской пластины, предполагая, что разность температур между потоком и поверхностью увеличивается линейно с расстоянием от переднего края. Людмила Фирмаль
Dx означает «вычислить с помощью x + Dx».Подставляя значения, найденные в уравнении равновесия импульса (2.1), получим: Дтр1>Лм—И Дхр’?|₁ь — / — I ’ Дхрсоз0 = 0 (2.7) поскольку r имеет одинаковое значение при 2 = 0 и 2 = b для каждого фиксированного значения x, то 3-й и 4-й члены приведенного выше уравнения отменяются. Далее мы делим оставшиеся члены формулы (2.7) на LI⁷Dx и передаем Dx к соответствующему пределу, указывая на ноль. И затем… (2-8) По определению, член*слева от последнего уравнения является всего лишь 1-й производной от x для X. Таким образом, выражение (2.8) можно переписать в виде: Таким образом, мы получаем дифференциальное уравнение для потока импульса th.
При интеграции вы увидите следующее: т » = р? hsov₽+ С1 (2.10)) Для определения интегральной постоянной используют граничные условия на границе жидкости и газа(раздел 2.1). 1 x x = 0 tv = 0 (2.11) Подставляя это граничное условие в уравнение (2.10), мы видим, что оно равно C₁= 0.Таким образом, распределение импульсного потока, показанное схематично на Рис.
- Выглядит следующим образом: Если рассматриваемая жидкость является ньютоновской жидкостью, как вы знаете, поток импульса связан с градиентом скорости следующей зависимостью: (2.13) Подставляя эту формулу в Формулу (2.12), получим следующее дифференциальное уравнение для распределения скоростей: (2.14) После того, как вы консолидируете последнее уравнение, вы можете легко получить его. (2.15) Используйте следующие граничные условия для нахождения интегральной константы.
Подставляя это граничное условие в уравнение (2.15), получаем C₂=(p ^ cos 2 [1] 62).Распределение скоростей принимает следующий вид (2.17) Таким образом, профиль скорости будет парабола(см. рис. 2-1). Когда вы найдете профиль скорости, вычислите некоторое количество, которое характеризует поток жидкости. 1.Максимальный знак скорости znax получается при x = 0, то есть,、 С05 Р 2р (2.18) 2.Средняя скорость по всему поперечному сечению слоя жидкости(.Ви? Значение (U) может быть определено в результате следующих расчетов: РГ созрела 3.Объемный расход жидкости (] может быть найден путем интегрирования средней скорости потока или распределения скоростей.
Затем он быстро переходит в турбулентный таким образом, что вЬкритической точке конвективная толщина турбулентного пограничного слоя равна конвективной толщине ламинарного слоя. Людмила Фирмаль
Толщина b может быть выражена как: средняя скорость, объемный расход или массовая плотность орошения (G = pb ): (2.21) 5.Величина 2-компонентной силы е, действующей со стороны жидкости на твердую поверхность, определяется интегрированием импульсного потока через границу раздела жидкости и твердой стенки. Lulug. = — LI’R (- ^°⁰3р)= rebI » soz US $(2.22) Нетрудно заметить, что найденное значение в точности равно 2 компонентам силы тяжести всей жидкости, образующей пленку. Указанное соотношение справедливо только в том случае, если пленка течет слоями и ее линии тока прямые. Эти условия соблюдаются при медленном осушении слоя вязкой грязи fluid.
Экспериментально установлено увеличение скорости жидкости с увеличением толщины пленки на 6 и уменьшением кинематической вязкости V = p / p. Характер течения также постепенно меняется. Вы можете наблюдать 3 более или менее четких режима устойчивого течения. б) ламинарное течение с волнами; в) турбулентное течение. Однако в настоящее время имеется мало количественных данных об ожидаемых моделях течения при фиксированных физических условиях.
Если жидкость стекает вдоль вертикальной стенки, можно дать следующую информацию[1, 2): Быть 44-25 если нет ламинарного потока Волнообразование Волна ламинарного течения 4 4-25 10004-2000 меньше Завихрение Быть> 10004-2000 Где He = 46 r₂ p / p-число Рейнольдса пленки жидкости. В следующей главе показано, почему эта группа параметров без размеров используется в качестве характеристики потока. Вязкость ПДК зависит от расстояния в зависимости от соотношения (2.23) го [(!++ «+*- Н-И И+ 4 4)]- Последнее выражение соответствует соотношению (2.17).
Смотрите также:
| Теория вязкости жидкостей | Течение в круглой трубе |
| Баланс количества движения в тонком слое. Граничные условия | Течение в кольцевом канале |

