Оглавление:


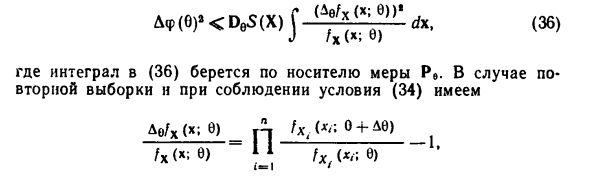

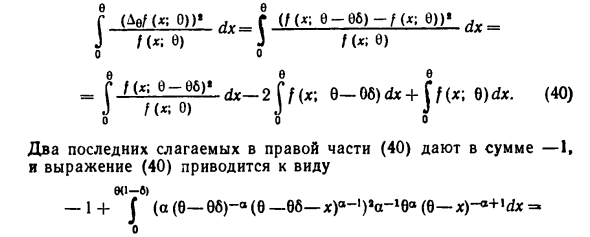


Границы дисперсии при нарушении условий регулярности
- Как видно из неравенства Фреше-Лао-Крамера, Нормальная дисперсия несмещенных оценок при повторной выборке При увеличении n он на порядок больше, чем n ~ K. Γ (Xn) имеет порядок 1 / l, а неравенство Чебышева имеет вид Отклонения от математических ожиданий Осеики Заказ 1 /) ‘i. В то же время, был нисходящий пример Дисперсия была равна 1/2. Так было и для образца равиомера @, 8) Распределение и статистика X („) и распределение Экспоненциальная плотность от a до exp ((* -μ) / °) и распределение 100 * Тыстики X (I).
Другими словами, точка останова функции распределения. Может быть показано Это, вообще говоря, точка xv ф. р. F (x; c) u есть Можно оценить по результатам дифференцирования и итерации 1 /) Отбор образцов с точностью выше ‘l. Здесь мы ограничиваемся Пример. (IV) Одномерное распределение передискретизации Интервалы @, a (9)) и ф сосредоточены. р. Вблизи точки F (x; c) x = a (B) работает следующим образом. 1-F (a (Q) -b, 9) -c6 °, 6-> 0, 0, c> 0. В этом случае пр »л -> — оо 194 (—кта). C0)
В обоих случаях разрывы оцениваются Плотность f {x; 9) распределение отдельных наблюдений или др. Людмила Фирмаль
Следовательно, поскольку отклонение X1P) от (9) равно rrUa, Если a <2, статистика x (n) является лучшей оценкой a (9) Это то, что вы обычно ожидаете. | Неравенство Фреше-Лао-Крамера можно исправить Следовательно, дисперсия оценки и Нарушение правил. Пишите в случае скаляра Условие для объективной оценки 5 (х) по параметру 9, пункты 9 и 5 9 + A9: JS (x) fx (x; 9) dx = (e)) Mx; 6) dx = 0; С2) I (S (x) -φ (9)) fx (x; G + Л6) dx = ф (в + Л6) -ФF), Где d \ = dx \ dxn, а интеграл понимается как одномерный. Вы — Вычитая уравнение С2) друг от друга, получаем: | E (x) -p (e)) Ae / x (x; c) -фφ (в). С3) Где Д9 / Х (х; 6) = / х (х; 6 + А9) — / х (х; в), АФ (9) = Ф (9 + А9) — Учитывая D9 {x: fx (x; 6 + A6)> 0} C {x: fx (x; 6)> 0}. C4)
Затем ограничьте область интеграции C3) вправо Установите C4) и перепишите C3) в следующий формат GE (x) -FF)) YV * ^? k («; c) A = A» p (c). C5) Неравенство Коши-Шварца-Бняковского применительно к С5), Мы получаем f 1UKH (X’U dx, C6) Здесь интеграл от C6) переходит в поддержку старшего Pv. В случае Повторная выборка с учетом условия C4) De / X (x; 6) L X / 195 Интеграл в правой части C6) можно описать следующим образом. Си (XI; E + выше) : C) J + L C7> С учетом независимости от диеты. с. Jf |, …, Xn, и это C7) Получить выражение ) С8) Равенство, подобное C7), Если i = 1, то для повторной независимой выборки Неравенство С6) имеет вид я ^ L) ‘) «-¦), 39) (V) Рассмотрим конкретный случай примера (IV).
- Плотность одномерного распределения передискретизации f (x; 9) = a9-α (e-x) a ~ \ 0 0 настроек. Это позволяет Одномерный вариант условия C4. Выполните основные преобразования Преобразование, мы получаем r (Ae / (; 0)) ‘dxГ (/ (; 8-86) -Hx; 0))’ dx_ Дж / (*; 0) Дж / (х; 0) Ой ой она = ГПх \ 0-06) ‘dx_2 [f (x; 9-06) dx + (/ (x; Q) dx. D0) J} {x \ 0) J J 0 0 0 Последние два слагаемых справа от D0) составляют в сумме –1 И формула D0) 90-6) -1+ f (aF-96) -aF-66-x) c- |) Chx-16bF-; о
-1 + fa (l-b) -M1-x) to- * (\ + bxA-x) -1I- ^. D1) о 6-I) показывает, что уравнение D1) эквивалентно sba. в — некоторые константы. Имея в виду это асимптотическое явление, Отбрасывая коэффициент (• —b) интеграла D1) и устанавливая y = \ -x, Напишите остальные выражения в си: те Я » 1-b) ‘- «- 1) dy = 6» a f (r + b) — «-‘ (A — = — zI» ^ -I) dz, Переменная 2 = 6 ./- ‘-b внесены изменения, Далее наше заявление 00 c = a j r — »- 1 (от A + yy до a-1) dz.
Возьми 6а = (бн) -1. b — произвольная постоянная. следующий C9) Людмила Фирмаль
Найти -1) — ‘^ D2) 0af ‘(GJ (bn) -2a ((c (bn) -1 + 1) «-1) ~ x- «(Ccb’1-1) -> n-2». D3) Значение b может быть выбрано, чтобы максимизировать D3 l-2 / коэффициент). Принимая ба порядка n ~ {+ t или n ~ ‘- *, e> 0, Легко видеть, что правая сторона D2) аккуратна oA) n-2a, где oA) — «0, I -» — oO. Следовательно, граница D3) является явной Лучшее, что вы можете дать (по порядку) Неравенство С9). Обратите внимание, что мы оцениваем параметры по Порядок статистики x (P), предложенный в примере (IV) время дает оптимальный порядок отклонения (см. C0).
Смотрите также:
| Скалярный параметр | Функция правдоподобия |
| Векторный параметр | Оценки максимального правдоподобия |
Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.

