Оглавление:




Графо-аналитический метод.
- Метод графического анализа. Метод интегрирования дифференциальных уравнений криволинейных осей основан на уравнениях отклонения и поворота угла поворота, с помощью которых можно рассчитать отклонение и угол поворота в любом сечении балки. Как и в случае сложных нагрузок, при работе с большим количеством участков, расчет при применении данного
метода достаточно трудоемкий. В этих случаях наиболее удобным может быть графический метод. С другой стороны, при решении некоторых задач (статически неопределенные балки, расчет максимального прогиба) целесообразно использовать графический анализ, чтобы в этих случаях увидеть прогиб и угол поворота только для некоторых конкретных участков.
Метод основан на подобии дифференциальной зависимости от силы прогиба, изгибающего Людмила Фирмаль
момента и непрерывного нагружения. Мы можем сделать любой луч и любую нагрузку Фигура. Двести девяносто шесть, (Инжир. 296). Дифференциальное уравнение для криволинейной оси этого луча (§ 109): (194) Под наш луч мы рисуем второй луч такой же длины, некоторую нагрузку, все еще неизвестную, непрерывную нагрузку qf, положительное направление, которое нужно принять; это устройство поддержки луча этот второй луч называется фиктивным
и фиктивным. h все значения, связанные с ним, обозначаются значком/. Для этой воображаемой балки значение изгибающего момента Mf в каждом сечении также вычисляется путем интегрирования с использованием метода анализа графов 376 и метода построения диаграмм [CHAP]. XIX в. Момент (19.2) Принимать Дифференциальные уравнения, связывающие изгиб и интенсивность непрерывного нагружения (§ 116)): д * МФ Сравним уравнения(19.1)и(19.2). Если То есть нагружают фиктивную балку
- фиктивной нагрузкой, которая изменяется по закону изгибающего момента реальной балки, после чего добиваются равенства любых констант слева и справа от выражения d2 (EJy) dMf dx-dx**., ____ то есть, SL=SP и OL = OP, получаем: d (EJy) _dMf9 -> } Но gi * А В Фигура. Двести девяносто семь б DX DX EJy=Mf. Учитывая, что Радж относительно y и mula, решение этих you-6 даст вам фору- } (19.3) 0= — 2z. ЭДЖ • Отклонение поперечного сечения фактической балки (от заданной нагрузки) равно изгибающему моменту в той же части фиктивной балки (от фиктивной нагрузки), деленному на жесткость фактической балки. (19-4)) Угол поворота фактической балки
(от заданной нагрузки) равен поперечной силе в том же сечении фиктивной балки, деленной на жесткость фактической балки. В аналитическом методе определения деформации были найдены произвольные константы при граничных условиях, т. е. равенство нулевого прогиба в опорном сечении и равенство деформации между ними в поперечном сечении, общем для двух соседних сечений балки. Возможно, метод анализа графов P7 удовлетворяет уравнениям (19.1) и (19.2), фиксируя концы (или промежуточные части) воображаемой балки.) (19.3) и (19.4): 1) если отклонение действительной балки f равно нулю, то в том же сечении мнимой балки мнимый изгибающий момент должен быть равен нулю;2) Если действительная балка F равна нулю, то мнимый изгибающий момент должен быть равен нулю.
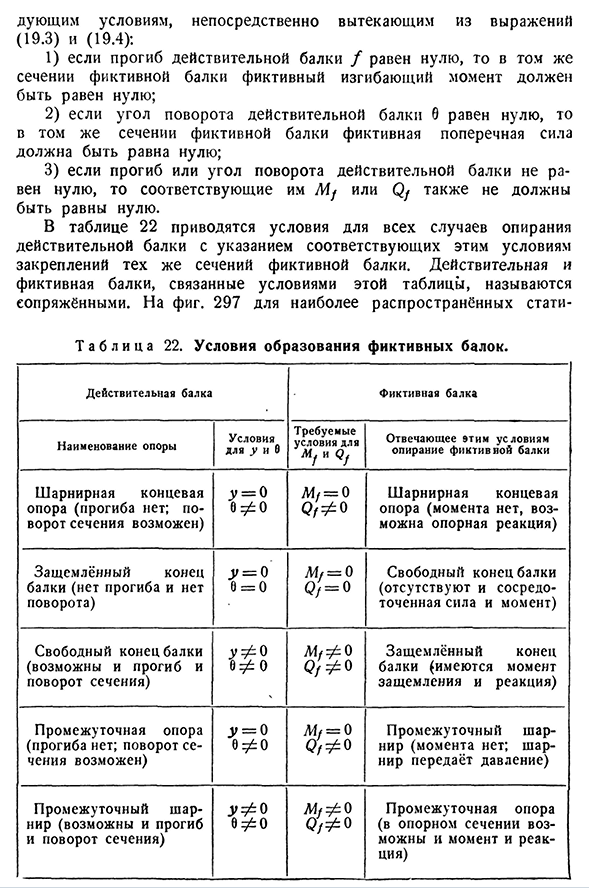
В таблице 22 приведены условия для всех случаев опоры реальной балки с указанием соответствующих Людмила Фирмаль
условий фиксации одной и той же части фиктивной балки. Реальные и мнимые пучки, Соединенные условиями этой таблицы, называются сопряженными. Как использовать для наиболее распространенных статей 297-Т А Б Л и с А22. Условия формирования воображаемого пучка. Эффективный луч-это воображаемый луч U и 9 поддерживают имена условий Обязательные требования к Али и Ду Опора для балок-манекенов, отвечающих этим требованиям Шарнирная краевая опора (без прогиба; поворот возможного поперечного сечения) 3″=около 6^0 L=0, поддержка конца шарнира(отсутствие вращающего момента, возможной реакции поддержки) Зажатый конец Луча(отсутствие отклонения и вращения) Макс=0 0=0 m,=о свободном конце луча (отсутствует концентрация и момент) Свободные концы балки
(возможен прогиб и поворот сечения) 0^0Q / ^0 Зажатый конец балки (с моментом дробления и реакции) Промежуточная поддержка (отклонение; никакое вращение раздела не возможно) _u=0 0^: 0 СЧ=0 средних суставов (отсутствие крутящего момента, давления, передаваемого совместной) Промежуточный шарнир (возможен и прогиб, и поворот секции) 0#: о компании Промежуточная опора (в справочном разделе возможны как момент, так и реакция) 378 анализ графа и графический метод[CHAP. XIX в. Комбинация реальных и вымышленных лучей показана в списке определяемых
лучей. В каждой паре сопряженных Пучков один можно считать действительным, тогда второй из них является фиктивным, что можно упростить, обратившись к таблице 22. Шарнирная многошпиндельная Балка позволяет выбрать сопряженную балку, как показано на рисунке. 298. Обратите внимание, что статически определяемый реальный луч всегда соответствует статически определяемому фиктивному лучу. Итак, для того чтобы найти отклонение y или угол поворота 0 любой части заданной (фактической) балки, необходимо последовательно выполнить следующие операции: a)); ’ 3 ~ ~ ~ & ——— £ Фигура. 298. В) для создания нулевой линии графика M (x)для фиктивной оси балки
и графика M(x)для фиктивной нагрузки qf\для положительного значения изгибающего момента покажите опору фиктивной балки согласно условиям отрицательного d) таблицы 22 и рисунков. 297 или 298; e) вычислить величину реакции опоры манекена балки от фиктивной нагрузки (т. е. реакции опоры манекена).; д) вычислить величину изгибающего момента M f в поперечном сечении фиктивной балки/;ж) вычислить величину поперечной силы Qf в поперечном сечении той же поперечной балки, в которой угол поворота равен 0. Графоаналитический метод определения
деформации освобождает нас от необходимости нахождения какой-либо константы в каждом конкретном случае, а данные в таблице приводятся уже на рисунке 22. 297 или 298 дают решение, которое соответствует определенному исходному условию. Мнимый момент-это размерность[Сила Х длина 3];мнимая боковая сила-[сила х длина 3]; Сила мнимой нагрузки измеряется в единицах-[Сила Х длина].
Смотрите также:
| Сложение действия сил | Примеры определения деформаций графо-аналитическим методом |
| Дифференциальные зависимости при изгибе | Графо-аналитический метод при криволинейных эпюрах изгибающего момента. |

