График функции

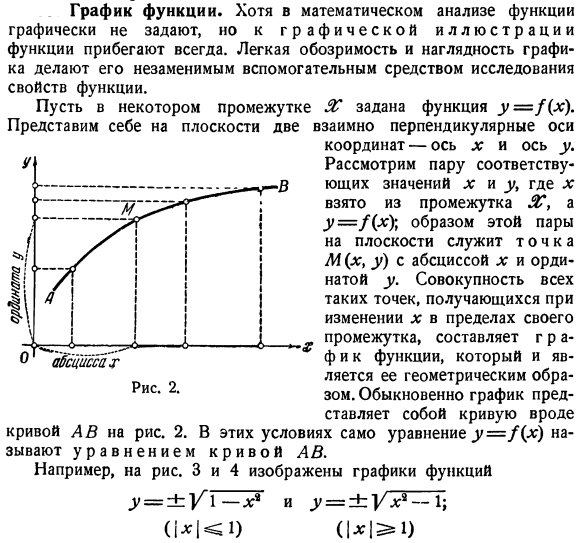
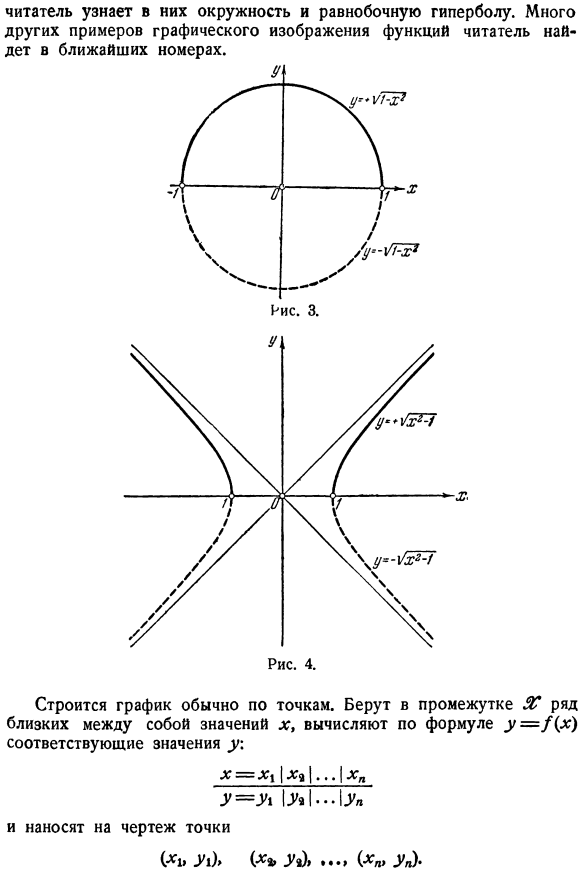
График функции

График функции. В математическом анализе функция не задается графически, но она всегда опирается на графическую иллюстрацию. Предположим, что функция y = f (x) задана в интервалах&.Представим себе 2 взаимно перпендикулярные оси на плоскости Координаты-оси x и Y. рассмотрим соответствующие пары значений x и _y. где x-интервал A? Он берется из и y = f (x).

Легкая видимость и визуализация графика делает его незаменимым вспомогательным инструментом для изучения свойств функций. Людмила Фирмаль

• Образ этой пары на плоскости-точка M (x> y) с абсциссой x и ординатой y. совокупность всех таких точек, возникающих при изменении x в этом интервале, образует график функции, являющийся ее геометрическим образом. График обычно представляет собой кривую, подобную кривой L B на диаграмме. 2.При этих условиях само уравнение y = f (x) называется уравнением кривой AB. И затем г =±г х * −1; (1 * 13 * 1） г =±г 1-НН (И<1） Например, на рисунках 3 и 4 показан график функций.

• Читатель узнает в них круг и равностороннюю гиперболу. Читатель найдет много других примеров графического представления функции в следующем вопросе. График обычно строится по точкам. Расстояние Нет. Возьмите значение X близко к и вычислите соответствующее значение y с формулой y = /(x). х = ХХ \ ХВ \ … \ хп г = г \ / а | … / А и поставить точки На чертеже ( • * ! Ыы)> г%)> *• * >(.хп> УП) Р.

Кривая рисуется с этими точками вручную или с помощью шаблона (с использованием определенного приближения, конечно), чтобы получить нужный график. Людмила Фирмаль

• Чем плавнее ход графика и чем плотнее точки На графике, тем точнее нарисованная кривая. Заметим, что геометрический образ функции всегда можно «вообразить», но не всегда, и этот образ будет кривой в обычном интуитивном смысле. Например, создадим график с функцией y = E (x). в интервале» [-2、-1）、[-1、0）、[0、1）、[1、2）、[2 、3）、… Функция является постоянным значением-2—1、0、1、2、…График состоит из большого количества независимых горизонтальных отрезка с правого края (Рис. 5)*).

Смотрите также:

Решение задач по математическому анализу

Определение понятия функции.	Функции натурального аргумента.
Аналитический способ задания функции.	Элементарные функции.