Графическое решение задач математического программирования
Самыми наглядными методами решения задач математического программирования являются графические, но они приемлемы только для функций двух и иногда трех переменных.
Рассмотрим пример: минимизировать
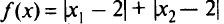
при ограничениях
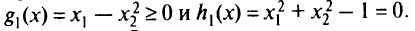
Таким образом, имеем задачу нелинейного математического программирования. Прежде всего построим по условиям ограничениям допустимую область 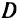 — множество точек
— множество точек 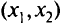 , удовлетворяющих ограничениям задачи. Ограничение
, удовлетворяющих ограничениям задачи. Ограничение 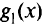 определяет область
определяет область
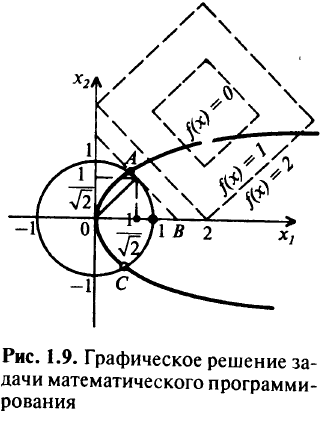
внутри параболы 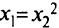 (рис. 1.9); ограничение
(рис. 1.9); ограничение 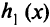 — окружность единичного радиуса с центром в начале координат. Допустимая область
— окружность единичного радиуса с центром в начале координат. Допустимая область 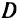 этой задачи — дуга окружности
этой задачи — дуга окружности 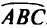 . Чтобы найти точку, в которой функция
. Чтобы найти точку, в которой функция 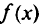 принимает минимальное значение на допустимой области
принимает минимальное значение на допустимой области 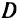 , построим линии уровня
, построим линии уровня 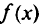 —штриховые линии. В точке (2.2)
—штриховые линии. В точке (2.2)
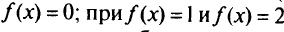
линии уровня образуют квадраты. Градиент функции 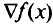 направлен в сторону дуги
направлен в сторону дуги 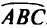 , и функция
, и функция 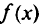 будет иметь минимальное значение в точке касания линии уровня к дуге
будет иметь минимальное значение в точке касания линии уровня к дуге 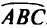 . Так как линии уровня отсекают от осей
. Так как линии уровня отсекают от осей 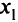 и
и 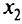 равные отрезки, то координаты точки касания равны
равные отрезки, то координаты точки касания равны
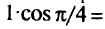
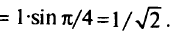
Решение задачи:
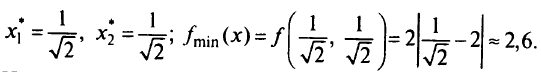
Нетрудно видеть, что то же решение будет и в том случае, если вместо 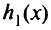 взять
взять 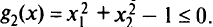 . Тогда допустимая область
. Тогда допустимая область 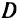 будет заключена между дугами
будет заключена между дугами 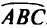 и
и 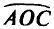 (см. рис. 1.9). Но минимальное значение функции
(см. рис. 1.9). Но минимальное значение функции 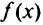 в области Сбудет достигнуто в точках
в области Сбудет достигнуто в точках
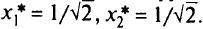
Рассмотрим второй пример: Пусть в задаче о питании (см. разд. 1.1)
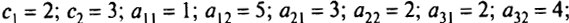
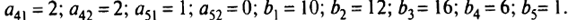
Получили задачу линейного программирования: минимизировать
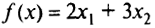
при ограничениях:
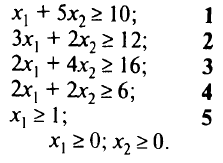
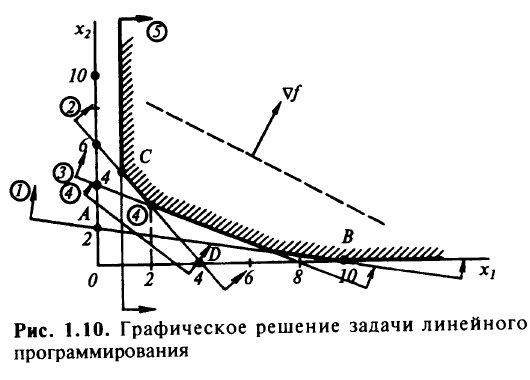
Построим области, определяемые неравенствами в ограничениях задачи (рис. 1.10). Сначала строим прямую 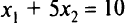 по двум точкам: пусть
по двум точкам: пусть 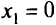 , тогда
, тогда 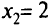 ; при
; при 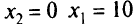 . Нанесем точки (0, 2) и (10, 0) на график и проведем прямую
. Нанесем точки (0, 2) и (10, 0) на график и проведем прямую 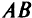 . Чтобы установить, какая часть плоскости определяется неравенством
. Чтобы установить, какая часть плоскости определяется неравенством 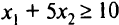 подставим в него координаты точки (0, 0). Получим противоречие, т. е. неравенство определяет полуплоскость, не содержащую точку (0, 0). Стрелки на прямой
подставим в него координаты точки (0, 0). Получим противоречие, т. е. неравенство определяет полуплоскость, не содержащую точку (0, 0). Стрелки на прямой 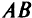 указывают эту полуплоскость. Аналогично строим области, соответствующие другим неравенствам. Неравенство
указывают эту полуплоскость. Аналогично строим области, соответствующие другим неравенствам. Неравенство 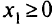 можно сразу исключить, так как оно «поглощается» неравенством
можно сразу исключить, так как оно «поглощается» неравенством 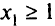 . Допустимая область
. Допустимая область 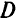 — заштрихованная выпуклая неограниченная многоугольная область. Чтобы найти оптимальную точку, построим одну из линий уровня целевой функции и ее градиент. Пусть
— заштрихованная выпуклая неограниченная многоугольная область. Чтобы найти оптимальную точку, построим одну из линий уровня целевой функции и ее градиент. Пусть 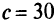 , т.е.
, т.е. 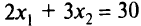 (штриховая линия), а градиент
(штриховая линия), а градиент 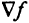 имеет координаты (2,3). Так как требуется определить минимальное значение
имеет координаты (2,3). Так как требуется определить минимальное значение 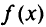 на области допустимых значений, то перемешаем линию уровня параллельно самой себе в направлении антиградиента до тех пор, пока она будет находиться в допустимой области. Точка «выхода» линии уровня из допустимой области и будет точкой, где
на области допустимых значений, то перемешаем линию уровня параллельно самой себе в направлении антиградиента до тех пор, пока она будет находиться в допустимой области. Точка «выхода» линии уровня из допустимой области и будет точкой, где 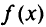 примет минимальное значение:
примет минимальное значение:
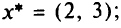
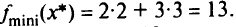
На рис. 1.10 видно, что задачи математического программирования могут не иметь решения либо иметь бесчисленное множество решений. Если бы при тех же ограничениях, какие были заданы в условии задачи, потребовалось максимизировать целевую функцию 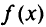 , то линию уровня пришлось бы перемещать в
, то линию уровня пришлось бы перемещать в
направлении градиента 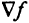 . Очевидно, в этом случае решения не существует — множество
. Очевидно, в этом случае решения не существует — множество 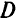 не ограничено.
не ограничено.
Теперь заменим целевую функцию задачи. Пусть требуется минимизировать функцию 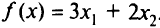 . Очевидно, что линии уровня будут параллельны прямой 2, т. е. линия уровня «выйдет» из допустимой области по отрезку прямой
. Очевидно, что линии уровня будут параллельны прямой 2, т. е. линия уровня «выйдет» из допустимой области по отрезку прямой 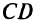 : все точки отрезка будут являться решениями задачи (бесчисленное множество).
: все точки отрезка будут являться решениями задачи (бесчисленное множество).
При решении задачи линейного программирования может оказаться, что ограничения противоречивы. Например, если ограничение 4 записать в виде 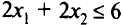 , то это неравенство будет описывать полуплоскость, включающую точку (0, 0), не имеющую общих точек с другими полуплоскостями (с решением неравенств 1, 2, 3). Решения в данном случае не существует.
, то это неравенство будет описывать полуплоскость, включающую точку (0, 0), не имеющую общих точек с другими полуплоскостями (с решением неравенств 1, 2, 3). Решения в данном случае не существует.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

