Оглавление:




Графическое представление моментов инерции
- Графическое отображение момента инерции Расчет момента инерции по формулам (2.45) или (2.43), (2.44) можно заменить простой графической структурой. В этом случае возникают прямые и обратные проблемы. Первый заключается в определении момента инерции для любой центральной оси z, y в известном направлении главной оси и величины главного центрального момента
инерции[формула (2.45) J. Известным моментом инерции J#JZy является уравнение (2.43), (2.44) и (2.38) 1 относительно любой системы с прямоугольной центральной осью. P R I m a I s a d A h a. необходимо определить моменты инерции J z для осей z, y, Jyy Jzy (рис. 31, А)
известны направление и величина направления главной Людмила Фирмаль
оси J u, Jv. Конечно, мы предполагаем, что Ju>Jv. Аналитическое решение дано по формуле (2.45). Графическое построение осуществляется следующим образом. Рассмотрим»геометрическую плоскость» и обратимся к ней во введении 27 прямоугольная система координат. На горизонтальной оси откладываем момент инерции оси (Ju, Jv, Jz, Jy и др.).Центробежный / CB (Jzy и др.), и вертикальная
ось. да что с тобой такое? При правильном масштабе мы откладываем начало координат от начала координат вдоль оси абсцисс (рис. 31, б) отрезок примерно A и S равен основному моменту инерции. Отрезок AB DETA пополам, в результате чего радиус SA и BC= = SA = точки описывают окружность, называемую кругом инерции. Для определения момента инерции относительно оси g его проводят под углом а к главной оси, а от центра окружности под углом 2А выполняют луч CDZ (положительный угол-против часовой стрелки). Покажем, что она равна оси Jzy>для момента инерции для
- данной оси z и центробежного момента для горизонтальной оси. DZKZ=CDZ sin2A= — и-J°sin2A. (2.46) формула (2.46), ОКГ=О В+против+СКГ-Л+4″(4-СП)+ +4-с°s2a по=4-4<1+С О s2a по)+4″и в<1-С О s2a по>= Иногда эту точку называют главной точкой или фокусом инерционного круга на 1, Двадцать восемь. =JTI cos2a — / — Jv sin2a. основываясь на Формуле (2.47) Ha (2.45), мы видим OKZ=J2. Так,
в соответствующем масштабе абсцисса точки инерционного круга дает значение осевого момента инерции и вертикальной оси центробежного момента. Для того чтобы получить значение момента инерции для оси Y9, которая перпендикулярна оси, положительный угол p-a+удерживается на главной оси h, а горизонтальная координата задней точки Dy (отрезка oku) от центра круговой балки ccy при определенном угле 2P=2 равна вертикальной оси этой точки ktydy дает нам значение момента инерции, которое имеет о
братный знак (—Jzy), соответствующий повороту оси на 90 градусов. Заметим, Людмила Фирмаль
что две взаимно перпендикулярные оси соответствуют двум точкам окружности(Dz. Dy) лежа на одном диаметре. Проведите прямую линию от точки Dz (пунктирная линия на рисунке. 31, Б) параллельно оси d, которой она соответствует. Точка M на пересечении с окружностью называется полюсом окружности с инерцией 1. Легко заметить, что линия, соединяющая полюс с любой точкой окружности, указывает направление соответствующей оси с этой точкой окружности. Укажем, например, что линии Ма дают направление главной оси И. Угол между осью и углом DZMA, как
вписано для построения угла ACDZ и равный полуцентровому углу ACDZ на основе той же дуги AD2, равен складке угла между осью и углом DZMA, т. е. Поэтому линия m, составляющая направление оси Z, является углом и параллельна оси I. О б р а т н а я с а д а н а. будем знать момент инерции J2, JI, J2y, поперечного сечения балки против нескольких систем Вертикальная ось z, y(рис. 32, а). Необходимо определить главный момент инерции и положение главной оси. Для определенности конструкции, Jz>Jy, J? г>0. Это позволяет: 32, б) построить точки Dz и Dy, соответствующие моменту
инерции осей z и Y. OKG—J z, oku=Jy, координаты-центробежный момент инерции, KZDZ-Jgo, KyDy-LSU. Так как обе точки принадлежат к одному диаметру, соединяя их, мы получаем центр инерциальной окружности. Из центра C нарисуйте окружность поперек абсциссы с радиусом CDZ=ccy=(2.48) точка a N B. действительно.: __ ОА = Оку+кус+с=дя+ + | / 4 = =4Il+а)+ 29ОБ = OKU4-to us-SV-Jy+ — | / +Jly= — 4-КА+А) — К (А) 2+4 / У Чтобы определить направление главной оси, постройте фокус инерционного круга. Для этого нарисуйте линию
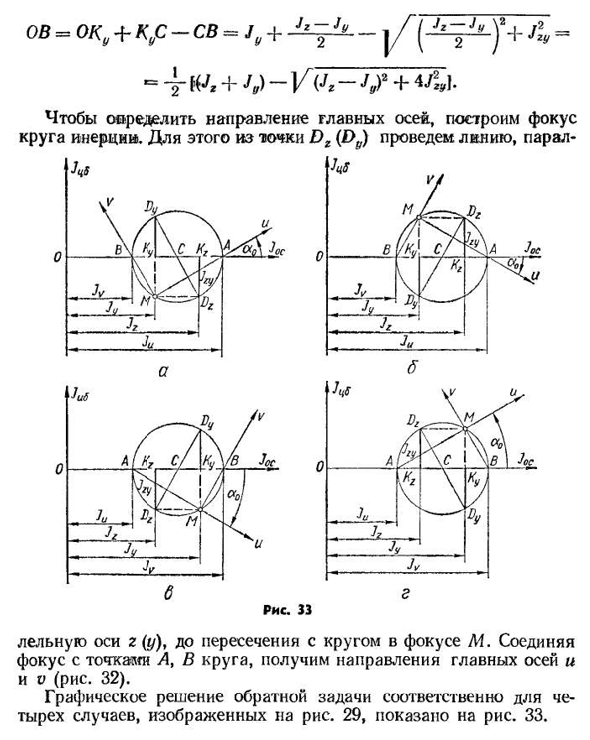
из точки D z (Dy Сфокусируйте лелоу ось z (y) на пересечении с окружностью фокуса M, сфокусируйте точку соединения A, окружность B, получите направление и главную ось v(рис. 32). Графическое решение обратной задачи, соответственно, будет описано в четырех случаях, показанных на рисунке. 29. 33.
Смотрите также:
| Зависимости между моментами инерции при повороте координатных осей | Понятие о радиусе и эллипсе инерции |
| Определение направления главных осей. главные моменты инерции | Порядок расчета |

