Оглавление:




Графический метод решения задачи
- Графический метод решения проблемы Рассмотрим проблему нахождения экстремального значения линейной дроби -ψτ „c \ x \ + c12 * 2 Функциональный Ζ = ——τ- MF \ X \ «ιC22x2 При некоторых линейных ограничениях. Bx \ x2 на плоскости Построить множество L возможных решений проблемы.
- Найти Функциональный экстремум достигается на пределе L. Выразите переменную X2 через x \ из уравнения (7). cu — Zc2X * 2 = 7 секунд W ^ bpl «-» подарок При использовании bZc k = ^ -, то предыдущее уравнение zc22 ~ s \ 2 Он принимает вид X2 = kx . Где k — угловой коэффициент линии * 2 = & * b зависит от Z. dk _ —c2 \ (^ c22 ~ «€ \ ϊ) -c22 (c \ ^ Zc2 ) s12c21-c \ 1C22 dZ ~ (Zc22-c12) 2 ~ (Zc22 ~ c, 2f ‘
Установить характер Возьми эту производную Людмила Фирмаль
Поскольку знаменатель полученной дроби всегда положителен, дк дк Поскольку числитель не зависит от Z, производная -p сохраняет знак Положительный или отрицательный. Следовательно, как Угловой коэффициент k увеличивается или Она уменьшается. Обратное также верно. То есть, если k увеличивается Функциональность только растет или уменьшается.
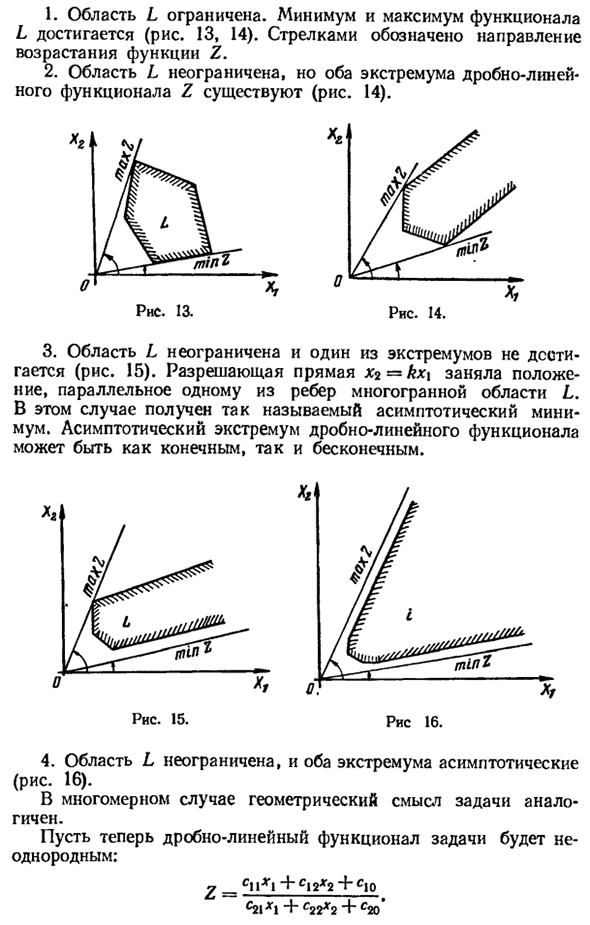
Так что найдите Увеличьте направление вращения, повернув прямую линию Xz = kx \ найти эти вершины вокруг начала координат 0 (0,0) Set L. Где крайнее значение линейной дроби Функциональная. При решении проблемы графическим способом, В следующих случаях: 116 1. Область L имеет границу. Минимальные и максимальные функции L достигается (Рисунки 13 и 14).
Стрелка указывает направление Увеличить функцию Z 2. Площадь L не ограничена, но обе крайности Существует линейный дробный функционал (рисунок 14). Рисунок 13. Рисунок 14. 3. Площадь L не ограничена, одно из крайних значений не ограничено Достигнуто (Рисунок 15). Линия решения Х2 = кх \ занято Положение параллельно одному из ребер многогранника области L.
В этом случае так называемая асимптотика Минимум Асимптотические экстремальные значения линейных дробных функционалов Либо конечный, либо бесконечный. Фиг.15. 4. Область L не ограничена, и оба крайних значения являются асимптотическими. (Рисунок 16). Если многомерный, геометрический смысл проблемы Это то же самое.
- Далее, линейный дробный функционал в вопросе Гетерогенный: C21 * l + c22 * 2 «f * C20 117 В этом случае многогранник L строится таким же образом. И линия разрешения вращается вокруг некоторого Точка A (x?, # 2), ее координаты: Метод. Измените переменную x \ = y \ — \ — x \ x2 = # 2 + * 2. Подставим эти уравнения для X1 и X2 для неоднородной функции Z. C \ Y \ + C \ 2U2 + SI *? + C12 * 2 + CU Z = A + I C2 \ Y \ + c22 ^ 2 + c21 * 1 + c22 * 2 «1» c20
Выберите координаты точки A, Новая переменная y \, y гетерогенного функционала теперь однородна Это c \ x \ + c \ 2x \ + sy = 0; c2 \ x \ + c22 * 2 + e = 0. (7) На самом деле в обоих случаях, то есть любой однородный Или гетерогенные функции, могут быть выполнены более легко, То есть не найти характер зависимости угла вычислить линейные коэффициенты разрешения и просто значения.
Линейная дробная функция при желаемом экстремальном значении Площадь L. Людмила Фирмаль
Затем выберите самый большой из числа приобретенных И самый маленький. Максимальные и минимальные значения соответственно Линейные дробные функции и соответствующие экстремумы Дело в том, что это лучшее решение. В обоих случаях мы рекомендуем вам проверить следующее: Знаменатель функции не исчез.
Для этого Наряду со строительством области L, это должно быть выполнено на самолете Строка, соответствующая знаменателю (C2i ^ i + c22 ^ 2 + C20 = 0) Функциональная. Эта линия не должна пересекать область. в противном случае Вы можете принять неправильное решение. Пример 1. Найти максимальное и минимальное значения функциональная 4ffitf Z = 3 *, -2 * 2 ~ 10 2χχ + x2 + 3
В условиях * -3 *! + 4 * 2 <13; x (+ x2> 5; 5xj —2 * 2 <и * Ho> 0. ,, L2 рисовый (8) (9) (10) Построить многогранник обычным способом L и прямой PQ (2dg, + x2 + 3 = 0) (рисунок 17). Линия PQ не пересекает L. Следовательно, функциональный знаменатель в области Ζ не исчезнет. узнать Координаты точки A (xj, * g) из системы Уравнение 1 типа (7) 3 *? -2x \ -10 = 0; 2 *? + * 2 + 3 == 0 29 дней.
Очевидно, х \ = у, а х2 =? -y- Отметить диаграммой. 17 баллов А, поворот 118 Решите прямую линию вокруг этой точки, чтобы найти ее предельное положение (Точки Топора и А2). Рассчитать значение функции в этих точках: -31-3-1-2.4-10 _ ~ 15 5 ^ * \ m1) -2-1 + 4 + 3-9 3 ‘ 2-5 + 7 + 3 ~ 20 » г Поскольку (Λ2)> Ζ {Αχ), maxZ = Ζ (Α2) == -gg, X1 opt = (5.7), minZ =
Смотрите также:
Примеры решения задач по математическому программированию

