Графический способ вычисления работы
Вычисление работы си ты на конечном пути по установленным формулам, без знания закона движения точки приложения силы, возможно лишь в частных случаях (например, при постоянной силе).
Для вычисления же работы силы в общем случае, когда сила может зависеть от времени, координат и скорости, нужно знать закон движения точки приложения силы. Только в этом случае можно выразить, как мы видели при решении задачи 86, все переменные в функции времени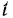 
и вычислить соответствующий интеграл.
Если же закон движения точки приложения силы неизвестен, то для вычисления работы силы нужно сначала найти этот закон, т. е. решить вторую основную задачу динамики.
На практике для определения работы часто пользуются графическим способом, используя для этой цели график зависимости
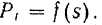
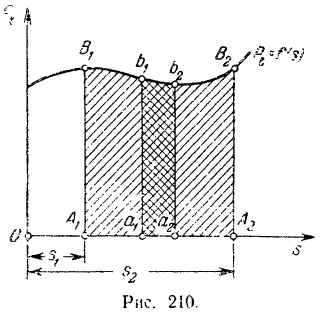
По оси абсцисс этого графика (рис. 210) отложены, в некотором масштабе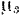 
значения дуговой координаты 
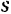точки приложения силы, а по оси ординат, также в каком-то масштабе 
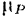, соответствующие им значения проекции этой силы на направление скорости точки 
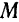, т.е.
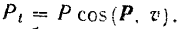
Элементарная работа силы будет равна
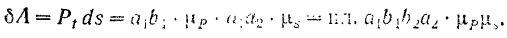
Работа силы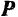 
на конечном перемещении ее точки приложения из положения 
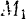с дуговой координатой 
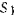в положение 
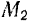с координатой 
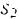будет выражаться в некотором масштабе площадью фигуры 
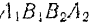(рис. 210):
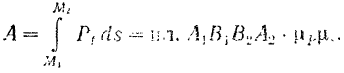
Работа силы на некотором перемещении ее точки приложения выражается в определенном масштабе площадью фигуры, ограниченной осою абсцисс, кривой
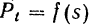
и двумя ординатами, соответствующими начальному и конечному положениям точки приложение силы.
На рис. 210 алгебраические значения касательной составляющей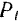 
силы отложены и положительную сторону соответствующей оси и потому работа силы 
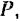изображаемая площадью фигуры 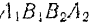, будет положительной. Если же построенная кривая
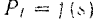
будет расположена от оси абсцисс в сторону отрицательных значений 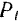, то соответствующая площадь будет изображать отрицательную работу.
К графическому способу определения работы силы приходится прибегать в тех случаях, когда нам известны значения силы 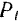только для отдельных значении 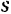, установление же аналитической зависимости
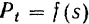
затруднительно или даже невозможно. В ряде случаев (например, при определении работы пара или газа в цилиндрах паровой машины или двигателя) график зависимости
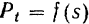
получается автоматически, при помощи самопишущих приборов, называемых индикаторами.
В заключение отметим следующее обстоятельство.
Хотя установленное в механике понятие работы (называемой иногда механической работой) и возникло из повседневного опыта, но оно не всегда совпадает с тем, что понимают под работой с физиологический точки зрения. Так, человек, неподвижно держащий па вытянутых руках тяжелый груз, не совершает, очевидно, с точки зрения механики, никакой работы (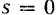
). С физиологической же точки зрения он совершает, конечно, определенную работу.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Элементарная работа силы |
| Работа силы на конечном пути с примером решения |
| Теорема о работе равнодействующей |
| Работа силы тяжести с примером решения |
