Оглавление:
Графический подход (метод координат)
При решении уравнения (неравенства) при помощи графического подхода в одной системе координат строятся графики функций, расположенных в левой и правой частях уравнения (неравенства). Затем ищутся точки пересечения этих графиков, после чего на оси абсцисс находится решение. В других случаях на плоскости 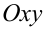 изображается геометрическое место точек, координаты которых
изображается геометрическое место точек, координаты которых 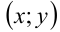 удовлетворяют заданным в задаче условиям, и это помогает в дальнейшем сделать решение задачи более наглядным и простым.
удовлетворяют заданным в задаче условиям, и это помогает в дальнейшем сделать решение задачи более наглядным и простым.
Возможные трудности связаны с необходимостью быстро и правильно строить графики функций с модулями, а также изображать фигуры на координатной плоскости в случае, когда уравнение или неравенство, их задающие, содержат модули. Необходимо при этом иметь навыки использования основных преобразований функций таких, как сдвиг графика вдоль координатных осей, его растяжение или, наоборот, сжатие, осевая и центральная симметрия. Надо уметь строить графические образы решений систем и совокупностей уравнений и неравенств, содержащих модули, раскрывая эти модули при помощи метода интервалов или, соответственно, метода областей и находя пересечение или объединение полученных в результате фигур. В качестве одной из иллюстраций данного подхода можно рассмотреть предыдущий пример.
Рассмотрим ещё несколько типичных примеров.
Пример №325.
При каких значениях параметра а уравнение 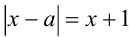 не имеет корней?
не имеет корней?
Решение:
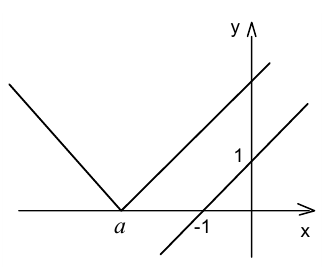
Построим в одной системе координат 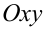 графики функций
графики функций 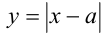 (это семейство «уголков» с вершиной, «плавающей» вправо-влево в зависимости от значения
(это семейство «уголков» с вершиной, «плавающей» вправо-влево в зависимости от значения 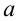 вдоль оси абсцисс) и прямая
вдоль оси абсцисс) и прямая 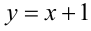 . Очевидно, графики этих функций не пересекаются (уравнение не имеет корней) при
. Очевидно, графики этих функций не пересекаются (уравнение не имеет корней) при 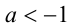 .
.
Пример №326.
Построить график функции
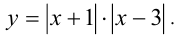
Решение:
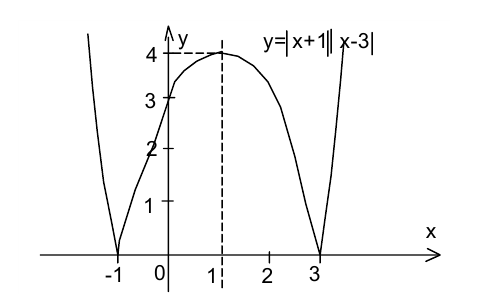
В данном случае проще всего преобразовать функцию к виду
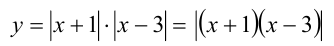
и построить параболу 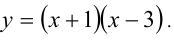 На участке между нулями этой функции
На участке между нулями этой функции 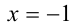 и
и 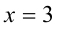 отобразим график вверх симметрично оси абсцисс. В результате получим искомый график функции. Он симметричен относительно прямой
отобразим график вверх симметрично оси абсцисс. В результате получим искомый график функции. Он симметричен относительно прямой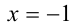 .
.
Пример №327.
Построить график функции
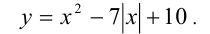
Решение:
Преобразуем данную функцию: 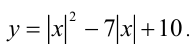
Пусть 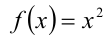
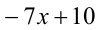 тогда исходную функцию можно представить в виде
тогда исходную функцию можно представить в виде 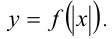
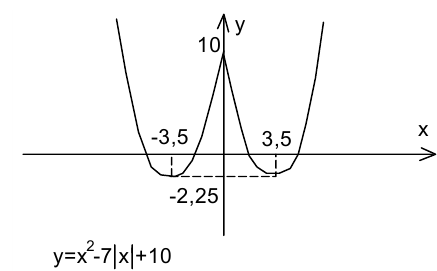
Для построения её графика достаточно вначале построить в области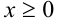 график функции
график функции 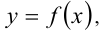 а затем отобразить эту кривую симметрично оси
а затем отобразить эту кривую симметрично оси 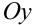 в область
в область 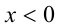 . Объединяя обе ветви кривых, получаем искомый график.
. Объединяя обе ветви кривых, получаем искомый график.
Пример №328.
Построить график функции
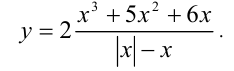
Решение:
Найдём область определения функции: 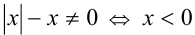 . Теперь упростим функцию на её области определения.
. Теперь упростим функцию на её области определения. 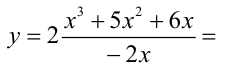
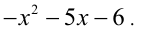
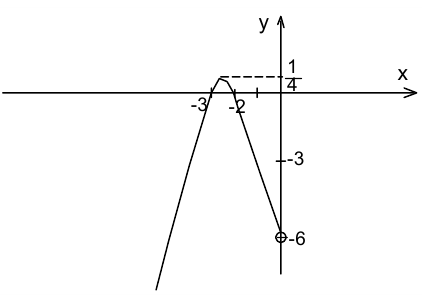
Графиком исходной функции будет та часть параболы (с вершиной в точке 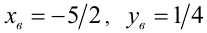 ветви направлены вниз), которая попадает в левую полуплоскость
ветви направлены вниз), которая попадает в левую полуплоскость 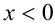 .
.
Пример №329.
Найти наименьшее значение функции
Решение:
Построим график функции методом интервалов.
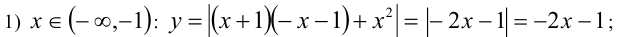
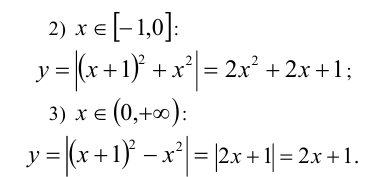
График состоит из трёх ветвей, объединённых в одну непрерывную кривую. По графику определяем, что
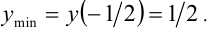
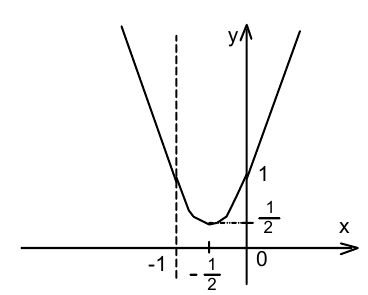
Пример №330.
Построить график функции 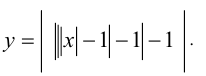
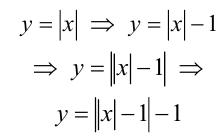
Решение:
Построим график при помощи двух преобразований: параллельного переноса вдоль оси 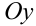 вниз на
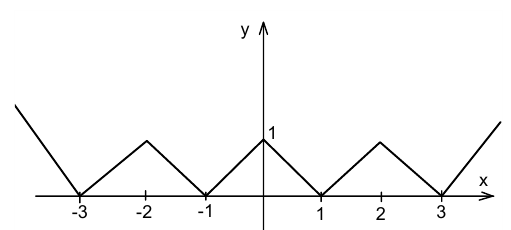
вниз на 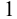 и графического «взятия» модуля. Для этого последовательно построим графики функций: и т.д. Эскиз искомого графика изображён на рисунке.
и графического «взятия» модуля. Для этого последовательно построим графики функций: и т.д. Эскиз искомого графика изображён на рисунке.
Пример №331.
Решить систему уравнений
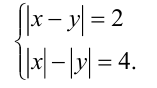
Решение:
Один из наиболее наглядных и быстрых способов решить данную систему уравнений — графический. Для этого достаточно изобразить в одной системе координат 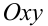 графики первого и второго уравнений системы. Тогда количество точек пересечения этих графиков будет равно количеству решений системы, а координаты этих точек будут решениями системы.
графики первого и второго уравнений системы. Тогда количество точек пересечения этих графиков будет равно количеству решений системы, а координаты этих точек будут решениями системы.
Чтобы построить графический образ первого уравнения, перепишем его в виде
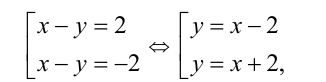
т.е. первое уравнение задаёт на плоскости две параллельные прямые.
Чтобы построить график второго уравнения, заметим предварительно, что поскольку при замене 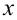 на
на 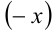 , а
, а 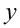 на
на 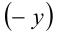 это уравнение на меняет своего вида, то фигура на плоскости, задаваемая этим уравнением, должна быть
это уравнение на меняет своего вида, то фигура на плоскости, задаваемая этим уравнением, должна быть
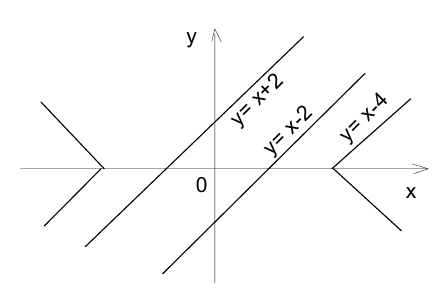
симметрична сама себе относительно обеих координатных осей. Поэтому достаточно построить, например в 1-й четверти, часть графика, а затем симметрично отобразить её относительно прямых 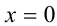 и
и 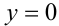 . В 1-й четверти
. В 1-й четверти 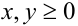 , поэтому модули раскрываются со знаком «плюс», и уравнение приобретает вид
, поэтому модули раскрываются со знаком «плюс», и уравнение приобретает вид 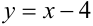 . Таким образом, в 1-й четверти второе уравнение задает часть прямой
. Таким образом, в 1-й четверти второе уравнение задает часть прямой 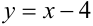 , в неё попадающую.
, в неё попадающую.
Симметричным образом достраивая фигуру на всей координатной плоскости, обнаруживаем, что графики первого и второго уравнений не имеют общих точек. Это означает, что система не имеет решений.
Замечание. Можно было воспользоваться для решения одним из известных свойств модуля, а именно, что 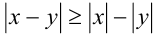 при всех действительных
при всех действительных 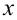 и
и 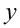 . В рассматриваемой системе, наоборот,
. В рассматриваемой системе, наоборот,
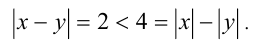
То есть условия системы вступают в противоречие с указанным свойством модулей, что также доказывает отсутствие решений у системы.
Пример №332.
При каких значениях параметра а модуль разности корней уравнения 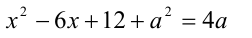 принимает наибольшее значение?
принимает наибольшее значение?
Решение:
Преобразуем уравнение к виду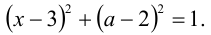
Введём на плоскости прямоугольную систему координат, на оси абсцисс будем откладывать значения переменной 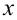 , а на оси ординат — значения параметра
, а на оси ординат — значения параметра 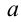 .
.
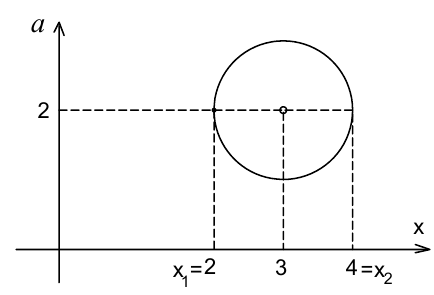
В этой системе координат уравнение задаёт окружность единичного радиуса с центром в точке (3;2). По рисунку видно, что модуль разности корней уравнения достигает наибольшего значения при 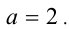
Пример №333.
При каких значениях параметра 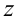 уравнение
уравнение 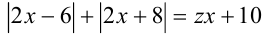 имеет единственное решение
имеет единственное решение 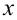 ?
?
Решение:
1-й способ. Поделим уравнение на 2:
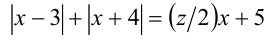
и обозначим выражение 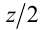 через
через 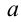 , а функцию в левой части последнего уравнения — через
, а функцию в левой части последнего уравнения — через 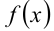 . Методом интервалов строим график функции
. Методом интервалов строим график функции
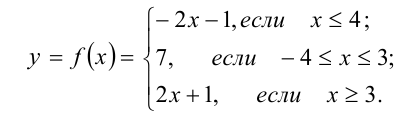
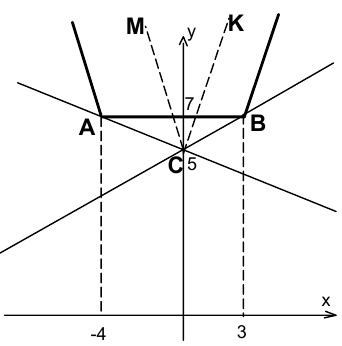
По условию задачи требуется найти все значения параметра 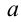 , при которых уравнение
, при которых уравнение
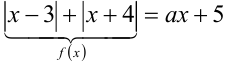
имеет единственное решение, т.е. графики функций 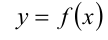 и
и 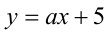 пересекаются в одной точке.
пересекаются в одной точке.
На рисунке график функции 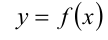 в виде ломаной линии выделен полужирной линией, графики
в виде ломаной линии выделен полужирной линией, графики
линейных функций 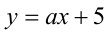 имеют вид пучка прямых линий (кроме прямой
имеют вид пучка прямых линий (кроме прямой 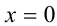 ), проходящих через точку
), проходящих через точку 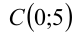 . Очевидно, что прямая вида
. Очевидно, что прямая вида 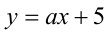 имеет единственную общую точку с ломаной линией лишь в следующих случаях.
имеет единственную общую точку с ломаной линией лишь в следующих случаях.
1) Прямая 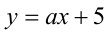 проходит через точку
проходит через точку 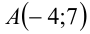 . Подставляя в уравнение прямой координаты этой точки, находим соответствующее значение параметра
. Подставляя в уравнение прямой координаты этой точки, находим соответствующее значение параметра 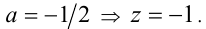
2) Прямая 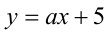 проходит через точку
проходит через точку 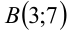 . Подставляя в уравнение прямой координаты этой точки, находим отвечающее ему значение параметра
. Подставляя в уравнение прямой координаты этой точки, находим отвечающее ему значение параметра 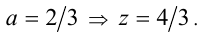
3) Прямая 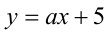 проходит параллельно левой ветви ломаной, т.е. совпадает с прямой
проходит параллельно левой ветви ломаной, т.е. совпадает с прямой 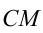 (её уравнение
(её уравнение 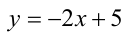 ), или имеет более вертикальное положение. Несложно вычислить, что указанным положениям прямой соответствуют угловые коэффициенты
), или имеет более вертикальное положение. Несложно вычислить, что указанным положениям прямой соответствуют угловые коэффициенты 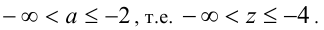
4) Наконец, прямая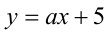 может проходить параллельно правой ветви ломаной, т.е. совпадать с прямой
может проходить параллельно правой ветви ломаной, т.е. совпадать с прямой 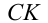 (её уравнение
(её уравнение 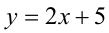 ), или иметь более вертикальное положение. В этом случае получаем для угловых коэффициентов следующий диапазон изменения:
), или иметь более вертикальное положение. В этом случае получаем для угловых коэффициентов следующий диапазон изменения: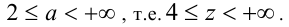 Объединяя полученные значения
Объединяя полученные значения 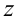 , приходим к ответу.
, приходим к ответу.
Ответ: 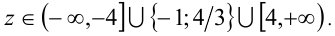
2-й способ. Воспользуемся методом интервалов.
1) 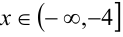 : уравнение принимает вид
: уравнение принимает вид 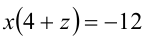 ; если
; если 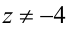 , то получаем единственное решение
, то получаем единственное решение
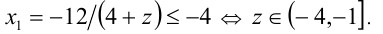
Итак, при 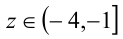 имеем решение
имеем решение 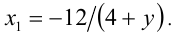
2) 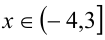 : уравнение принимает вид
: уравнение принимает вид 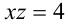 ; если
; если 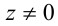 , то получаем решение
, то получаем решение 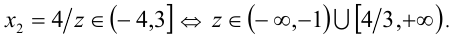
Итак, при 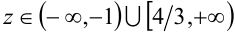 имеем решение
имеем решение 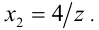
3) 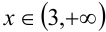 : уравнение принимает вид
: уравнение принимает вид 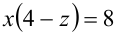 ; если
; если 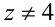 , то получаем решение
, то получаем решение 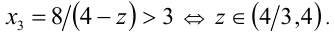
Итак, при 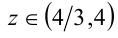 имеем решение
имеем решение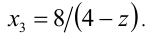

Объединяя полученные результаты, получим тот же ответ.
Пример №334.
Решить систему уравнений
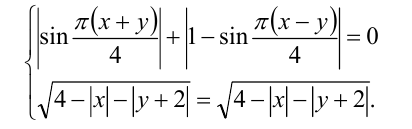
Решение:
Сведём систему к равносильной системе
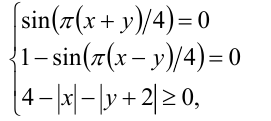
и сделаем замену переменных: 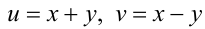 . Тогда получим
. Тогда получим
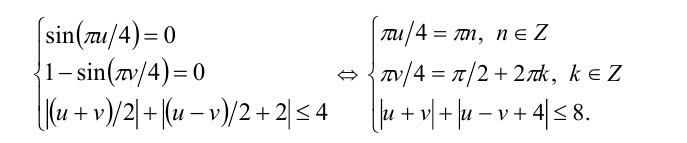
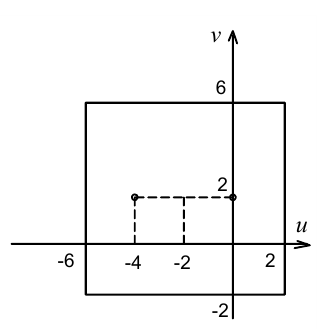
Неравенство последней системы описывает на координатной плоскости 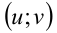 квадрат с центром в точке
квадрат с центром в точке 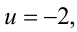 и
и 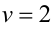
сторонами длиной 8, параллельными осям координат (см. рисунок). Среди бесконечного числа точек 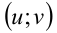 координаты которых удовлетворяют уравнениям системы, в этот и квадрат попадут лишь две:
координаты которых удовлетворяют уравнениям системы, в этот и квадрат попадут лишь две:
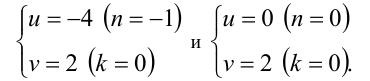
Отсюда, возвращаясь к первоначальным переменным, находим
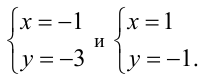 Ответ:
Ответ: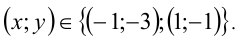
Пример №335.
Для каждого 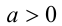 найти наибольшее значение величины
найти наибольшее значение величины 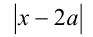 при условии
при условии 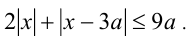
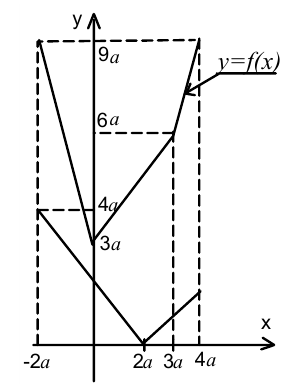
Решение:
Для решения задачи воспользуемся графическим подходом.Обозначим 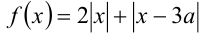 и построим график этой функции. Из рисунка видно, что неравенство
и построим график этой функции. Из рисунка видно, что неравенство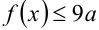 выполняется на отрезке
выполняется на отрезке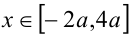 . Наибольшее значение функции
. Наибольшее значение функции 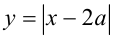 , судя по её графику, изображённому ниже на том же рисунке, достигается при
, судя по её графику, изображённому ниже на том же рисунке, достигается при 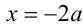 и равно
и равно 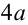 . Ответ:
. Ответ: 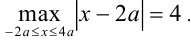
Пример №336.
При каких значениях 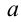 уравнение
уравнение 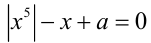 имеет единственное решение? Решить это уравнение для всех найденных значений параметра
имеет единственное решение? Решить это уравнение для всех найденных значений параметра 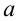 .
.
Решение:
Перепишем уравнение в виде 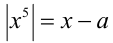 . Уравнение имеет единственное решение тогда и только тогда, когда графики функций
. Уравнение имеет единственное решение тогда и только тогда, когда графики функций 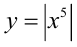 и
и 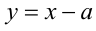 имеют единственную общую точку
имеют единственную общую точку 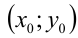 , т.е. когда прямая
, т.е. когда прямая 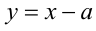 касается графика
касается графика 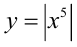 (или, что то же самое, графика
(или, что то же самое, графика 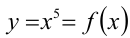 ). Угловой коэффициент касательной равен
). Угловой коэффициент касательной равен 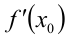 , а, с другой стороны, он равен 1. Таким образом, имеем уравнение
, а, с другой стороны, он равен 1. Таким образом, имеем уравнение
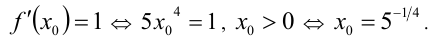
Следовательно, 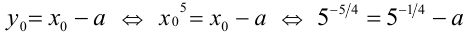 , откуда
, откуда 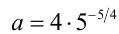 . Ответ: при
. Ответ: при 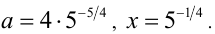
Для получения дополнительного опыта решения задач с параметрами рекомендуем обратиться к специализированным пособиям, например [14,24,25].
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

