Оглавление:
Графический подход (метод координат)
Основное достоинство графического подхода к решению задачи — это, как уже отмечалось выше, его высокая наглядность, а естественное ограничение в применении этого метода состоит в сложности построения графиков входящих в уравнение или неравенство функций. Часто с помощью графического подхода оценивают количество решений в задаче. Найденные «на глазок» при помощи построения графиков решения подлежат обязательной проверке. Если графически решается уравнение или неравенство с одним неизвестным, то, как правило, в одной системе координат строятся графики функций, расположенных слева и справа от знака равенства (неравенства), и затем с помощью этих графиков ищется решение.
Пример №363.
Решить уравнение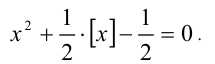 
Решение:
Перепишем уравнение в виде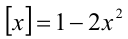 
и решим его графическим способом.
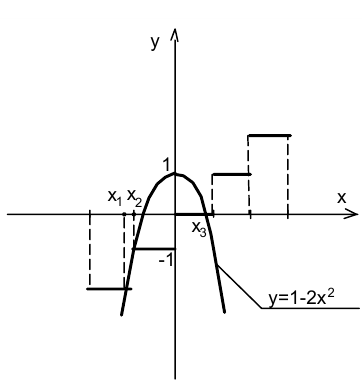
Построим в одной системе координат графики функций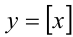 
и 
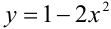, расположенных в левой и правой частях уравнения. На рисунке правые концы отрезков прямых линий на графике функции 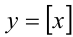считаются «выколотыми». Хорошо видно, что графики пересекаются в трёх точках, абсциссы которых удовлетворяют ограничениям: 
, 
, 
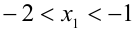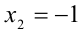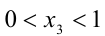. Один корень 
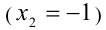находится сразу, а другие два пока что лишь локализованы, и требуется найти их точные значения. Чтобы найти корень 
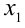, отметим, что на интервале — 
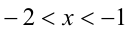, которому принадлежит этот корень, целая часть 
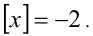Подставляя это значение в уравнение, получим 
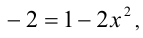откуда легко теперь находим корень 
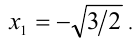Аналогично на промежутке 
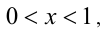которому принадлежит корень 
, 
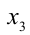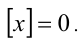Подставляя в уравнение, получаем 
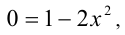откуда определяем 
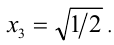Ответ: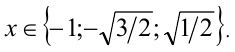 
В следующем примере не требуется вводить вспомогательную систему координат — она задана по условию задачи. Это так называемый тип задач «на построение ГМТ» (чаще практикуется на устных экзаменах по математике).
Пример №364.
Построить на плоскости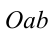 
геометрическое место точек
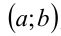, при которых у уравнения
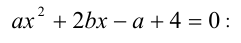
а) нет решений; б) ровно одно решение.
Решение:
а) Если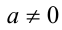 
, то уравнение квадратное, и соответственно оно не имеет решений тогда только тогда, когда его дискриминант 
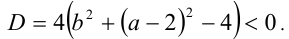На плоскости 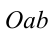это неравенство задает открытый круг (граница — окружность — ему не принадлежит) с центром в точке 
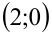и радиусом 2. Если же 
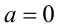то уравнение становится линейным 
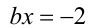и не имеет решений при 
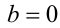. На плоскости 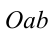это даёт точку 
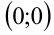— начало координат. Объединяя открытый круг и точку, получим ГМТ (см. рис. а)).
б) При 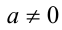квадратное уравнение имеет ровно одно решение тогда и только тогда, когда 
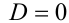; это уравнение задаёт на плоскости 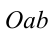окружность с центром в точке 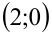и радиусом 2. Учитывая условие 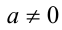, выкалываем на этой окружности точку 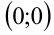. Если же 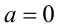, то линейное уравнение 
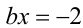имеет единственное решение при 
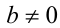. Это задаёт на плоскости вертикальную прямую, совпадающую с осью ординат. На этой прямой надо выколоть точку .
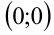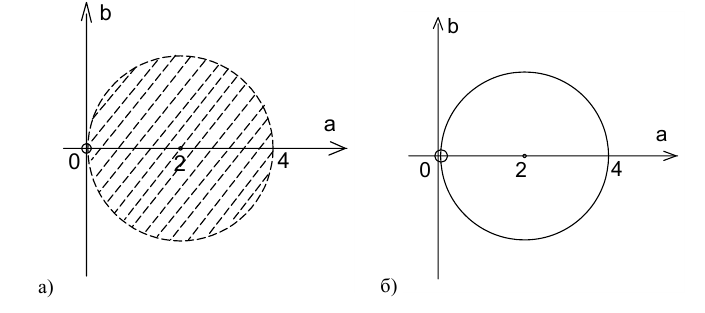
В итоге получаем следующую фигуру, состоящую из объединения указанных окружности и прямой (с выколотой точкой начала координат). Задача решена.
Графический подход часто оказывается удобен и при решении уравнений (неравенств, систем) с двумя неизвестными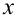 
, 
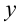, а также тогда, когда в задаче имеются неизвестная 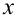и параметр 
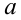. В первом случае вводится система координат 
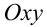с осями, на которых откладываются значения неизвестных 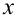, 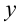. Во втором случае также вводится вспомогательная система координат, но на осях уже откладываются значения неизвестной 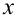и параметра 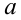. В обоих случаях решение видно наглядно в виде некоторого геометрического места точек координатной плоскости.
Пример №365.
При каких значениях параметра 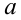модуль разности корней уравнения 
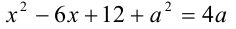принимает наибольшее значение?
Решение:
Решим задачу с помощью метода координат. Вначале, выделяя полные квадраты как по 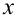, так и по 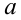, перепишем уравнение в виде
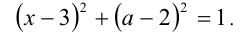
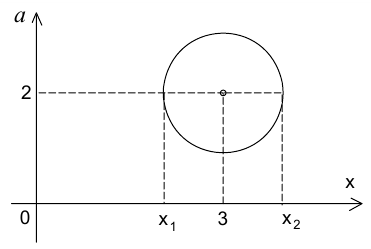
Введём систему координат, в которой на оси абсцисс будем откладывать значения переменной 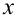, а на оси ординат — значения параметра 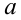. В такой системе координат уравнение задаёт окружность единичного радиуса с центром в точке 
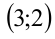. По рисунку видно, что, какое бы значение 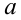в пределах от 1 до 3 мы ни зафиксировали, уравнение имеет корни 
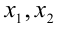, расположенные на оси абсцисс. Очевидно, что расстояние между этими корнями максимально и равно диаметру окружности при 
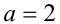(соответствует центру окружности).
Пример №366.
При каком значении 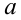система
имеет единственное решение?
Решение:
Приведём систему к виду
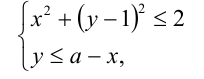
1 у < а — х,
и рассмотрим графическую интерпретацию неравенств системы на плоскости 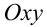. Первое неравенство задаёт на координатной плоскости замкнутый круг с центром в точке 
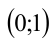и радиусом 
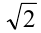. Второе, линейное, неравенство определяет полуплоскость, состоящую из точек плоскости, лежащих не выше прямой 
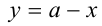(граница полуплоскости).
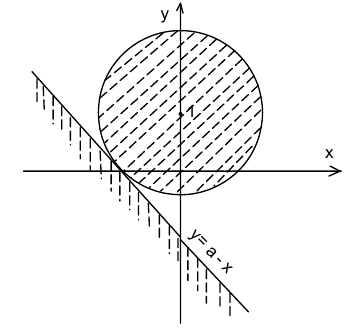
Уравнение 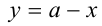задаёт семейство параллельных прямых, зависящих от параметра 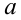. Система неравенств имеет единственное решение тогда и только тогда, когда окружность 
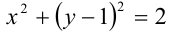касается прямой 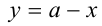так, как это изображено на рисунке. В этом случае система уравнений
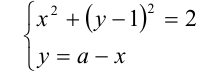
должна иметь единственное решение. Подставляя в первое уравнение вместо 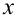выражение 
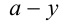, приходим к квадратному уравнению
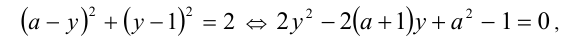
которое также должно иметь единственное решение. Это выполняется лишь в случае, когда его дискриминант равен нулю:
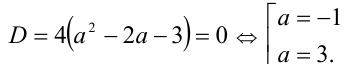
При этом значение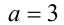 
не удовлетворяет условиям задачи (круг будет лежать в полуплоскости). Ответ: при 
.
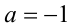Пример №367.
При каких значениях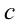 
уравнение 
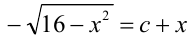имеет единственное решение?
Решение:
График функции в левой части уравнения
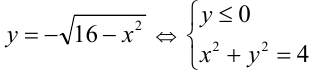
задаёт нижнюю полуокружность с центром в начале координат и радиусом 4 (сделайте чертёж самостоятельно), а график правой части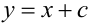 
— семейство прямых, пересекающих ось ординат в точке 
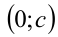под углом 
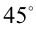. Эти графики имеют ровно одну общую точку 
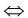прямая 
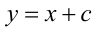либо касается снизу полуокружности (в этом случае её уравнение будет 
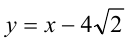(докажите), либо лежит между прямым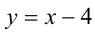и 
и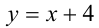 
(может совпадать с последней). Таким образом, 
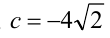или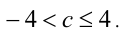 
В следующем примере графический подход используется для нахождения области допустимых значений неизвестных.
Пример №368.
Найти все целочисленные пары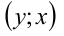 
, удовлетворяющие уравнению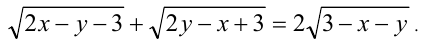 
Решение:
Найдём ОДЗ уравнения: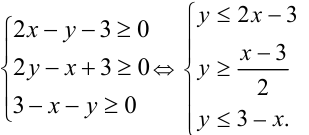 
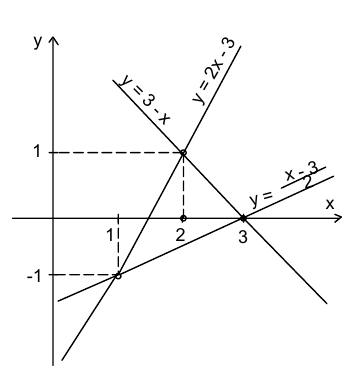
Данные три неравенства задают на координатной плоскости треугольник, внутрь которого попадают только четыре точки с целочисленными координатами: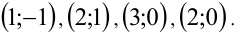
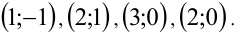
Проверкой оставляем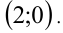 
Пример №369.
Определить, под каким углом видно из начала координат (т.е. внутри какого угла с вершиной в точке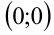 помещается) множество, заданное на координатной плоскости неравенством
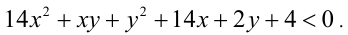
Решение:
Обозначим множество, заданное в условии неравенством, через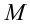 
. Заметим, что прямая 
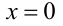не пересекает множество 
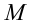, так как неравенство 
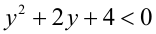не выполняется ни при каких 
.
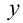Выясним, при каких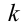 
у прямой 
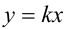есть общие точки с 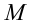, т.е. когда имеет решения система
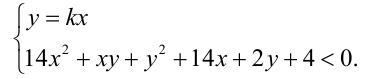
Подставляя вместо 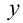выражение 
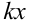в неравенство системы, получим
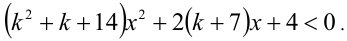
Это квадратное неравенство имеет решения тогда и только тогда, когда его дискриминант положителен:
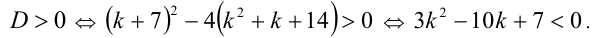
Решением последнего неравенства является интервал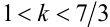 
. При этом в 
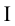четверти координатной плоскости нет точек 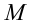, так как при 
, 
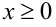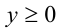левая часть неравенства не может быть отрицательна. Следовательно, множество 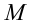расположено в 
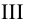четверти, и угол, под которым это множество видно из начала координат, равен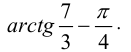 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
