Оглавление:
Градиент
Рассмотрим функцию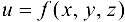 
, определенную в области D.
Определение 19.1. Говорят, что в области D определено скалярное поле, если для каждой точки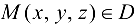 
задано некоторое число (скаляр), т. е.
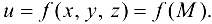
Таким образом, функция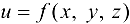 
— числовая функция точки.
Пример 19.1.
Температурное поле; распределение концентрации вещества в растворе.
Определение 19.2. Говорят, что в области D определено векторное поле, если для каждой точки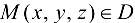 
задан некоторый вектор, т. е.
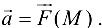
Пример 19.2.
Силовое поле, создаваемое некоторым притягивающим центром.
В каждой точке области D, в которой задана функция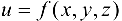 
, определим вектор, проекциями которого на оси координат являются частные производные 
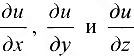этой функции в соответствующей точке:
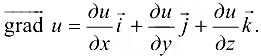
Этот вектор называется градиентом функции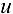 
.
Обозначение: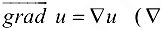 
— набла).
Таким образом, скалярное поле, задаваемое функцией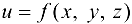 
, порождает векторное поле — поле градиентов 
.
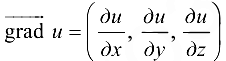Теорема 19.1. Пусть дано скалярное поле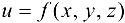 
и в нем определено поле градиентов. Тогда производная 
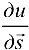по направлению некоторого вектора 
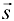равна проекции вектора 
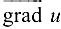на вектор .
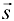Доказательство.
Рассмотрим единичный вектор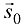 
, соответствующий вектору :
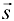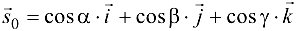
Вычислим скалярное произведение векторов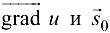 
:
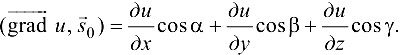
Правая часть формулы (19.1) — производная функции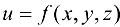 
по направлению вектора 
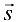. Следовательно, 
.
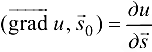Если обозначить угол между векторами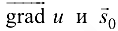 
через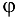 
, то можно записать:
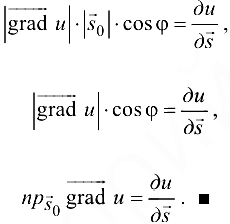
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
