Оглавление:
Градиент скалярного поля и его свойства
В каком направлении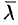 
производная 
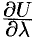имеет наибольшее значение? Это направление указывает вектор, называемый градиентом скалярного ноля.
Можно заметить, что правая часть равенства (70.2) представляет собой скалярное произведение единичного вектора
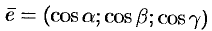
и некоторого вектора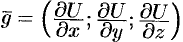 
.
Вектор, координатами которого являются значения частных производных функции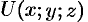 
в точке 
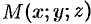, называют градиентом функции и обозначают 
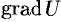, т. е. 
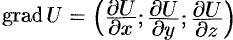или
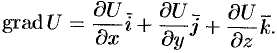
Отметим, что 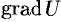есть векторная величина. Говорят: скалярное поле 
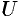порождает векторное поле градиента 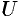. Теперь равенство (70.2) можно записать в виде
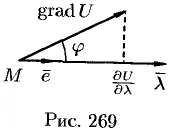
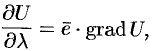
или
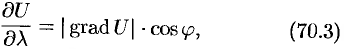
где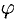 
— угол между вектором 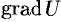и направлением 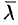(см. рис. 269).
Из формулы (70.3) сразу следует, что производная но направлению достигает наибольшего значения, когда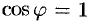 
, т. е. при 
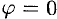. Таким образом, направление градиента совпадает с направлением 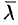, вдоль которого функция (поле) меняется быстрее всего, т. е. градиент функции указывает направление наибыстрейшего возрастания функции. Наибольшая скорость изменения функции 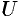в точке 
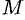равна
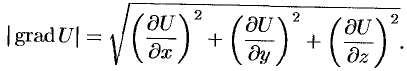
В этом состоит физический смысл градиента. На указанном свойстве градиента основано его широкое применение в математике и других дисциплинах.
Приведем важные свойства градиента функции.
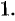Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
Действительно, по любому направлению вдоль поверхности уровня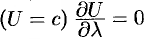 
. Но тогда из (70.3) следует, что 
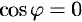, т. е. 
.
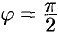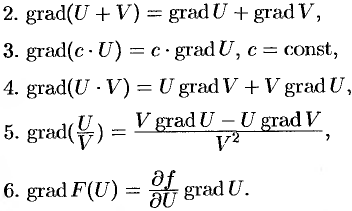
Доказываются эти свойства на основании определения градиента. Докажем, например, последнее свойство. Имеем:
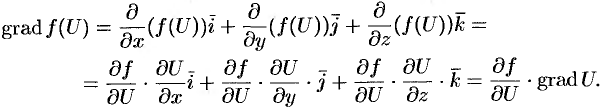
Замечание. Приведенные свойства градиента функции остаются справедливыми и для плоского поля.
Пример №70.2.
Найти наибольшую скорость возрастания функции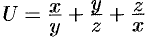 
в точке 
.
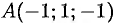Решение:
Имеем:
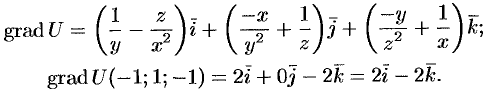
Наибольшая скорость возрастания функции равна
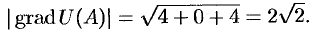
Отметим, что функция будет убывать с наибольшей скоростью 
, если точка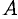 
движется в направлении — 
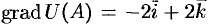(антиградиентное направление).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Комплексная форма ряда Фурье |
| Интеграл Фурье |
| Дивергенция поля. Формула Остроградского-Гаусса |
| Циркуляция векторного поля |
