Задача №19.
Горизонтальные колеса I и II дифференциального механизма вращаются вокруг одной и той же вертикальной оси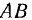 
соответственно со скоростями 
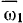и 
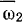. Определить мгновенную угловую скорость вращения планетного колеса III, ось которого может свободно вращаться вокруг оси 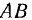(рис. 60).
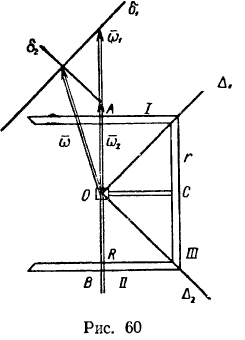
Решение:
Абсолютное мгновенное движение колеса III можно представить как результат сложения -переносного движения (вместе с колесом I) и относительного движения колеса III по отношению к колесу I. В таком случае переносная угловая скорость колеса III равна 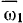. Перенесем начало вектора 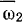в неподвижную точку и рассмотрим относительное движение колеса III. В этом относительном движении мгновенная ось вращения 
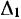колеса III проходит через точку соприкосновения колеса III с колесом I и через точку 
пересечения осей колес III и I. Поэтому конец вектора абсолютной угловой скорости расположен на прямой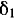 
, проходящей через конец вектора 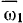и параллельной прямой 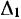Представляя теперь мгновенное движение колеса III как результат сложения переносного движения (вместе с колесом II) и относительного движения колеса III по отношению к колесу II, аналогичными рассуждениями получим, что конец вектора абсолютной угловой скорости колеса III лежит на прямой 
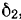, параллельной прямой 
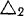, проходящей через конец вектора 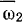. Величина- вектора абсолютной угловой скорости колеса III определится из простого геометрического построения и тогда
где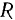 
и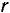 
— соответственно радиусы колес I и III.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
