Оглавление:




Главные оси и главные моменты инерции
- Основные оси и главный момент инерции. Из рассмотрения круговой диаграммы, видно, что это Суи! д) теория момента инерции оси 216, где центробежный момент равен двум взаимно
перпендикулярным[гл. VIII Нулевой и осевой моменты принимают максимальное и минимальное значения.
Эти оси называются главной осью инерции, а соответствующий оси момент-главным Людмила Фирмаль
моментом инерции. Предположим, что у нас есть самый большой момент, а J-самый маленький. Формулы для них: * Л,2=±± — дя)*+4Jlu, Т Г 2а,.2=4-4. J x J y (100.1) Где a-угол между осями x и 1. Эти формулы мы получили из уравнений (46.7)и(46.8) для определения главного напряжения и угла направления главной оси, через Jy и через JY
заменили их Oh через Jx, а X ясно, что круговая диаграмма действительно вырождается в точки может иметь только пару главных осей. Из любых соображений, если известно, что фигура имеет несколько пар главных осей, круговая диаграмма вырождается в точку, и любая ось является главной осью. Это относится главным образом к центральной оси всех правильных форм.
- Так, Момент инерции квадрата относительно любой оси, проходящей через центр тяжести, равен A4 / 12, Если a-сторона. На самом деле в квадрате можно указать две пары осей симметрии: прямую линию, соединяющую диагональ и середину стороны. Если ось является осью симметрии, как показано в § 96, ось является главной осью. Главная центральная ось и момент инерции имеют особое значение в теории изгиба. Чаще всего фигуру можно разделить на простые фигуры-прямоугольники и треугольники.
Схема определения главной центральной точки выглядит следующим образом: 1. Центроид фигуры расположен, а вспомогательные центральные оси x и y заданы. 2. Через центр тяжести каждой детали ее координаты находятся на оси x, y, x t, y t и параллельны оси z, t//, оси X и y. 3. Определяется квадратный момент инерции j {z (каждой детали относительно ее центральной оси и T). 4. Общий момент инерции диаграммы для осей X и y определяется следующим уравнением: J x= Дя=Е(4+ * Л). HHU^2 (Искусство! X{Y • (100.2)§ 100] шпиндель и главная инерция 217 5.
Уравнение (100.1) определяет угол A z для определения главного момента инерции и направления оси 1. Людмила Фирмаль
Для уточнения вопроса о том, какой осью является формула (36.9), относительно момента инерции имеем вид: t g». = — r^r= — Z если 2£ — (от 1 0 до 3 ) J х• ’ * й ху П р и М ЕР. Попробуем определить главный центральный момент инерции участка, показанного на рисунке. 145. Фигуру можно считать состоящей из трех частей: прямоугольника высотой 6 см и шириной 2 см, квадрата со стороной 4 см, крутого отрицательного участка диаметром ZCM. Чтобы выполнить первый этап, введите вспомогательные оси и v (вы можете выбрать в следующей таблице: как вам нравится). Путем расчета-
Т А Б Л И К А я И; Vi FT » I Fl F, I1 3 12 12 36 11 ′ 4 4 16 64 III3 4 — 7 — 2 1 — 28 21 55 72 Здесь Vj-координаты центра тяжести каждой детали, F {- площадь детали, ut Ft и ViF {- статический момент. Суммируя соответствующие столбцы, находим общую площадь для оси и ее статические моменты.: ,, _ С у имп_ 5 5_ _ _ л АО см H> ______ Н4 4см ia-2^, — Ji-CM’—— 21— О, * 6 см. Где x (- и, — и», Y1=1) {- va, момент инерции прямоугольника равен моменту инерции 218 [гл. VIII Формула (98.3): нет. СГ _ _ НВ*. Jx j2>J y J2 > std * момент инерции окружности равен (98.5), а для окружности площадь и осевые
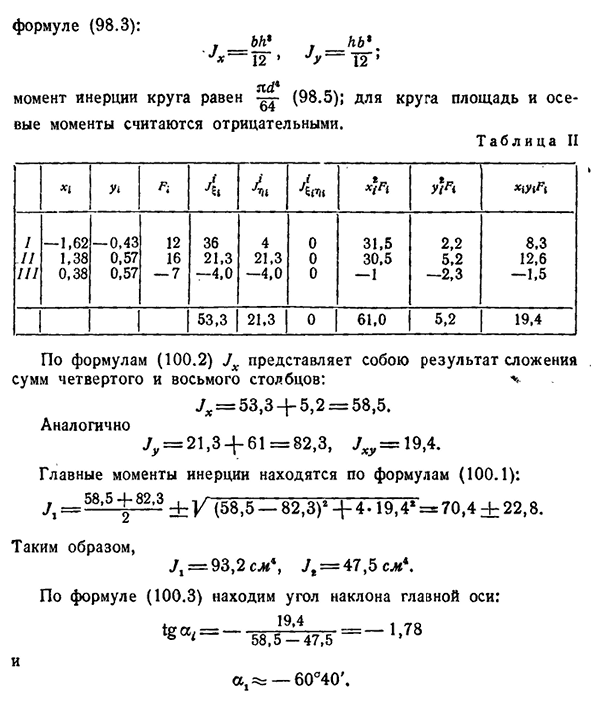
* * Иф ю/а>ул Я есть— 1,62 — 0,43 12 36 4 0 31,5 2,2 8,3 II1.38 0.57 16 21.3 21.3 0 30.5 5.2 12.6 III0,38 0,57 — 7 −4,0 −4,0 0 — 1 −2,3 −1,5 53.3 21.3 0 61.0 5.2 19.4 По формуле (100.2) Jx является результатом сложения суммы четвертого и восьмого столбцов:%Jx=53,3+5,2=58,5. Аналогично Jy= 21,3 + 61 = 8 2,3, J xj,=19.4. Основной момент инерции определяется по формуле(100.1): = 5 8,5 + 8?.’?’+ / (58,5 — 82,3)2 + 4 — 19,4 = 70,4 ± 22,8. Таким образом, Y1=93,2 SL*, J t=47,5 см\по формуле (100,3) находим угол наклона главного вала: *. Да.~ 5 8,519-4,47,5 ~ 1. 1_7 на 8Q И −60°40′.
Смотрите также:
| Вычисление моментов инерции | Действие поперечных сил на балку |
| Преобразование моментов инерции при повороте осей | Гипотеза плоских сечений и принцип Сен-Венана |

