Оглавление:




Главные центральные осевые моменты инерции простых сечений
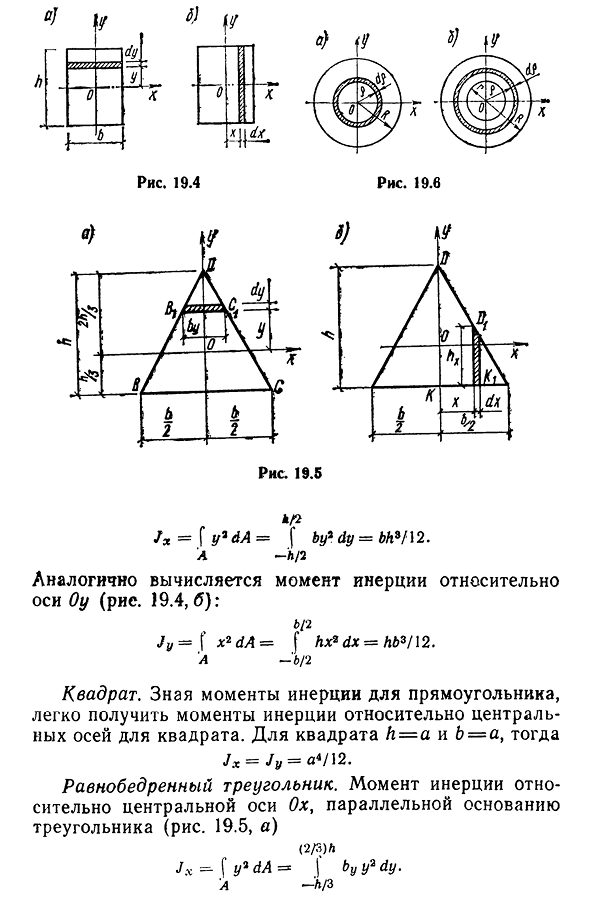
- Рассмотрим основные центральные оси моментов инерции простых сечений, таких как простые фигуры, прямоугольники, квадраты, треугольники, круги и кольца. Прямоугольники мысленно рассекают прямоугольник на множество горизонтальных полос, параллельных
оси ox, чтобы определить момент инерции/x относительно центральной оси ox и толщину dy(рис. 19.4, а). Основная площадь каждой полосы-dA=bdy. Рассмотрим один из них на расстоянии y от оси ox. Подставим значение dA в выражение (19.1): 197/3 = f y »
dA=f by1 off=bh9f\2. A-h / 2 Точно так же и момент инерции (рис. 19.4, б): B / 2 Людмила Фирмаль
Jy — \x2dA=(hx2dx=hb3 / \2. A ~ b / 2 Зная момент инерции квадрата, прямоугольника, легко получить момент инерции относительно центральной оси квадрата. Если квадраты h=a и B=a, то Jx=Jy=a* / \2. Равнобедренный треугольник. Момент инерции к центральной оси оси, параллельной основанию треугольника(рис. 19.5, а) (2/3) л Jx —
\y2dA= * f по y2dy. A~h / 3 Ширина полосы определяется из подобия треугольников BOC и B\DC\by=bll2hf3-y)/h, а при присвоении ей интеграла、 Момент инерции (рис. 19.5, б) S ‘ 2 Jy.И. х? = 2fx2hx ДХ. А0 Ширина полосы hx также определяется из подобия соответствующего треугольника DCK. И D\CK.\ ‘ .hx==2h(b / 2-x) / b. После подстановки в Интеграл получаем Два p i(L И В случае окружности окружности сначала вычисляют полярный момент инерции, а затем, через него,
- определяют момент инерции относительно центральных осей Oh и Oh. Толщина dp (рисунок) и вырезать круг в набор колец. 19.6, а). Площадь базового кольца, расположенного в точке p, вдали от центра окружности, равна d4=2npdp. Полярный момент инерции окружности Р j=[P2dA=[P2 2 lrrf=lya4 / 2. И Момент инерции окружности относительно центральной оси jx^jv = jp / 2=l/?4/4 Кольцо разрезают
также кольцами на множество колец, толщиной dp(рис. 19.6, б). Базовая площадка ringda=2npdp. Момент инерции полярности кольца /p=J P2dA=[P2 2 LRF=l(/?4-Г4) / 2. А момент инерции кольца относительно центральной оси Oh и Oh равны: (/?4-Г4) / 4.
Для диаграммы с двумя или более осями симметрии,оси- Момент Людмила Фирмаль
инерции относительно центральной оси перпендикулярны друг другу, одна из которых совпадает с осью симметрии и равна друг другу: Jx=J y==const, то есть квадрат, круг, кольцо и равносторонний треугольник. Величина момента инерции прокатного сортамента: углов, швеллеров, двутавровых балок и др. Принимается в соответствии с таблицей ГОСТ.
Смотрите также:
Решение задач по технической механике

