Оглавление:








Гипотеза Фридмена о постоянном доходе
- Гипотеза Фридмана о связях Первая модель адаптационных ожиданий была предложена Ф. Кейганом, Его известное приложение определенно является моделью потребления, Ванна по гипотезе Фридмана о фиксированном доходе (Friedman, 1957). Это было В этой модели индивидуальный / Период / обозначенный Cpjn предполагается пропорциональным константе.
- Новый доход Ypt;. C / 7 = RU / G (10,39) Кроме того, фактическое потребление Cit и фактическое. 1 Это значение зависимости (M / F) применяется только к небольшим значениям £ m. Например, есть Когда = 1% или 0,01, скорость изменения значения (M / P) t составляет e0> (ML-1, т.е. -0,046, Или -4,6%. Если £ m = 10%, т.е. 0,1, скорость изменения стоимости (M / P) t e-odb8_ i ttot_ _o, 374 или -37,4%, а не -47%.
Пример очень неточных чисел: формат строки для расчета скорости изменения. Людмила Фирмаль
Уровень дохода Yit включает компоненты времени C \ и Y \ соответственно. На самом деле, это зависит от ситуации года £ Cit = C? T + Cjt- (10,40) G = G / H G /. (10,41) Временные составляющие потребления и временный состав Переменная дохода является случайной величиной со средним значением 0, Постоянное значение дисперсии распределено независимо Постоянный доход, постоянное потребление и ранг друг друга.
Значение постоянного дохода в уравнении (10.39) не может быть соблюдено. О решении М. Фридман Изменения облигаций зависят от процесса ожидания адаптации. если Фактический текущий доход индивидуума выше (или ниже), чем постоянное значение Заработок в предыдущем периоде увеличился (или уменьшился) у физических лиц em) Последнее значение умножается на разницу, соответствующую X: АУ / = МУ / 7-У / Г_1). (10.42)
В общем случае значение X предполагается равным 0. И 1. Физические лица корректируют признание облигаций по мере их роста Хотя это фактическая сумма дохода, Фактические изменения дохода могут быть связаны с колебаниями времени Компонент дохода. Выражение (10.42) можно переписать как tf-jtfWO} / -tf-i>. (S.43) или Yif = XYit + (\ -X) Yll. (10.44) Это уравнение легко интерпретировать.
Инди оценка Тип постоянного дохода за год t равен средневзвешенному Это не предварительная оценка текущего фактического и постоянного дохода. если Если значение X близко к 1, человек на самом деле Доход, а значение Yp сразу приближается к K, в отличие от значения X Почти нулевой вес относительно реального дохода относительно Процесс корректировки идет медленно.
Подстановка значения Cpit уравнения (10.40) в (10.39) дает следующее: С / г-С ^ ру /, (10.45) или C ,, = ptf + Cj. (10.46) В результате фактическое потребление и С \ играет роль случайного члена. Это не было в модели. Заменить фактическую приведенную стоимость дохода 299 «Об индикаторе постоянного дохода при принятии определенной гипотезы Как указано в разделе, доход не разрешается давать ле 8.3, смещение, неверные оценки параметров.
Вместо М. Fried- Мужчины использовали уравнение (10.44) для оценки связей и их отношений Фактическое значение дохода для текущего и прошлого. Конечно, уравнение (10.44) Не может использоваться напрямую для измерения стабильного дохода Две причины в год: я не знаю значение Х Для?
Вторая причина — формула (10.44) Он удерживается для периода /, а затем также для периода (/ -1). 1 £, = ^ 1 + 0-ЩГ (-2- (10,47) Подстановка этой формулы в (10.44) дает: Yf = XYit + X (l-Щм + (1-X) 2Y, l2 (10,48) Конечно, это уравнение содержит ненаблюдаемую компоненту Ypjr_2, Вы можете удалить выражение (10.44), сместив его на 2 периода. (10.48), чтобы получить зависимость Ypit от Yjr Yit_v Yjt_2, Ypit_y
Повторяя эту процедуру бесконечно, Ypit можно выразить следующим образом. Сумма текущих и прошлых фактических значений дохода: Y, T = XYit + X (1-X) Yit. {+ X (1-X) 2Y / 7_2 + X (1-X) 3Yit_3 + …. (10.49) Основываясь на разумном предположении, что значение X находится на графике От 0 до 1 мы можем заключить, что (1-X) находится на той же границе. Следовательно, (1-X) s уменьшается с увеличением s.
Это Что текущая стоимость дохода имеет наибольший вес, значение до дохода Вес предыдущего периода низок, и значение этого веса постепенно Уменьшается при возвращении в отдаленный прошлый период. в Со временем становится очень мало и все предыдущие Вы можете игнорировать соображения. Тем не менее, проблема оценки количества X остается. Аналогично решению Жена Ф. Кейгана в своем исследовании гиперинф Отношения.
Он испытал ряд различных значений Х от 0 до 1 Соответствующая серия каждого фиксированного дохода построена Уравнение зависимости потребления для ряда постоянных данных Выручка с использованием коэффициента R2 для измерения качества оценки. Тогда он Выбранное значение X Это получает серию Yp и лучший.
- Ваша оценка Свойства динамической модели Динамические свойства модели Фридмана полезны для последующего анализа. Осуществление конвертации кроватей. Предположим, вы хотите использовать агрегацию Данные шины и, следовательно, индекс / могут быть опущены. Заменить выражение (10.44) становится (10.46): С, = р ^ + Р (1-Х) Г £ + С, р. (10.50) Сдвиг формулы (10.45) на один период вперед дает: tYtix = Ct_x-Clx. (10.51)
Подстановка этой формулы в (10.50) дает: Ct = VkYt + (\ -X) Ct_x + Cj to (\ -X) Cj_x. (10.52) Эта формула допускает как краткосрочные, так и долгосрочные Общая тенденция потребления. Краткосрочные маржинальные тренды Расход dCt / dYt равен коэффициенту Yn, то есть RA.
Компонент (1-А) СМ Поскольку Yr не может измениться, краткосрочный аспект функционирует как константа. Людмила Фирмаль
Может влиять на значение С м Что произойдет, если сумма дохода меняется со временем? Будет ли оно постепенно увеличиваться? Увеличение выручки в этом году Косвенное потребление в этом году В следующем году (1-X) значение SG будет болезненным в следующем году Чем текущий. Другими словами, график функции потребления смещается Up.
Если выручка продолжит расти в будущем, функциональная схема сместится Кроме того, общие отношения между потреблением и доходом Еще больше в доме 10.1 с пунктирными линиями на рис Круче, чем краткосрочная зависимость. и (1-X.) Ссылка Y, YU1 Yu2 Y Рисунок 10 1. Динамические свойства постоянных моделей Доход Фридмана Зависимость состояния длительного равновесия кроме случайного.
Термин может быть получен путем подстановки C, = St_x = C и Y, = Y в выражение. (10.52): C = pxG + (1-MS, (10,53) Можно упростить до следующего формата: 301 с = пр (10,54) Модель сводится к постоянному потреблению зависимости Фридмана. Доход со свободными членами, равными нулю и равным коэффициентом наклона Угол наклона краткосрочной функции (Вт, Значение A находится между 0 и 1.
Поэтому модель Фридмана Объясните сосуществование краткосрочных тенденций предельного потребления Средний тренд ниже 1 и почти постоянный После войны до потребления это было загадкой эконометрики STV. Однако модель Брауна, показанная в упражнении 10.7 Приводит к подобным уравнениям. Вот пример два раза радикально.
Личная экономическая модель, которая приводит к таким же отношениям между Запустите наблюдаемую переменную. Кроме того, Уравнение поведения удовлетворяет условию Гаусса-Маркова и становится Даже коричневая модель кровати устраивает, Модель Фридмана, он отрицательно коррелирует с ним Поэтому MNC не применяется.
В пудинге Этот вывод является основой для выбора модели, Причины полагать, что случайные члены в уравнении действия не являются Это мотивация для выбора 100 моделей после удовлетворения требований Это не будет принято. случай Чтобы сравнить версию функции потребления с другими функциями ми М. Фридман США на душу населения и реальный располагаемый доход на душу населения.
Исключая военное время с 1905 по 1951 год (Фридман, 1957, с. 142— 152). В пошаговом поиске он рассчитал величину фиксированного дохода следующим образом: Сумма текущей стоимости дохода и предыдущей стоимости 16, и оптимальная Значение Х составило 0,37. В уравнении функции потребления он Получили значение р = 0,88. В результате краткосрочные маржинальные тренды.
Потребление составило 0,33, а краткосрочный множитель — 1,5. доллар Долгосрочные показатели составили 0,88 и 8,5 соответственно. движение 10,10. Исследователи считают, что стоимость одежды определяется следующим образом: По модели: logy, = <x + p, log *, + P2logp, + u, (1) Где yr — стоимость одежды (1 млрд. Долл. США, постоянная цена), z — постоянная.
Новый доход; p} — фактический индекс цен на одежду ( Мухи). Исследователи также считают, что определенный доход зависит от фактов Выручка хр по следующему уравнению: Общее значение n и значение задержки: вес этой зависимости следует за полиномом Распространение. По этой причине журнал Almon также хорошо объяснен.
Как задержка в полиномиальном распределении. Вот простой пример Да, значения веса следуют за квадратичной зависимостью (Рисунок 10.2A и 10.2B) Кубическая функция или полином высокого порядка (как на рисунке 10.3) Штрафы. Выбор функции зависит от исследователя и, конечно, он Создано на основе экспериментов.
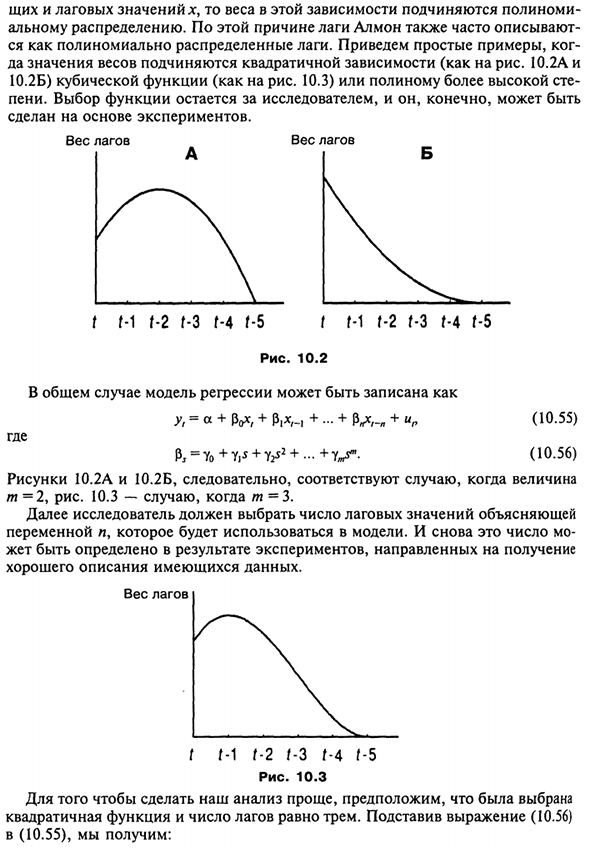
Вес бобы Вес бобы A I B ф М ф-2 ф-3 ф-4 ф-5 т М ф-2 ф-3 ф-4 ф-5 Рисунок 10.2. В целом, регрессионная модель может быть записана как yt = a + PoXf + p ^, + … + P „x, -„ + Lp (10.55) где P ^ Yo + V + Y ^ + .-. + Y ^ — (S-56) Поэтому на рисунках 10.2A и 10.2B указано количество м = 2, рис. 10,3-м = 3 Далее исследователь должен выбрать количество значений задержки для объяснения Переменная n используется в модели.
И снова это число мо Могут быть определены в результате экспериментов, направленных на приобретение Правильное описание доступных данных. Вес я ф м ф-2 ф-3 ф-4 ф-5 Рисунок 10.3 Чтобы сделать анализ проще, Квадратичная функция с 3 лагами. Замена выражения (10.56) (10.55) будет: 304 y, = a + px, + p, x, , + p2x, _2 + pz *, -s + yi = = «+ VL + (Vo + Y, + Y2) * / -1 + (Y0 + 2Y, + 4Y2) V2 + (Yo4» 3Yi + 9Y2) * / -s + u = = a + y0 (x, + x ^ j + x ^ 2 + x ^) + Yi (Vi + ^ r-2 + 3 VB) + Y2 (*, -i + 4 V 2 + 9 *, -h) + wr = = <* + Y (10,57) Где ZQ = *, + V l + * / -2 + *> — 3> * 1 = Vl + 2 chl-2 + 3 * g-3 И * 2 = * rl + 4xr-2 + 9 xl- 3 ‘
Для оценки параметров модели необходимо построить уравнение зависимости не из текущего значения и значения задержки lg, а из изменений, построенных из них нью-йорк Большинство статистических программ могут сделать это легко. С ними Вы можете использовать его для получения коэффициентов построенной переменной.
На их основе рассчитывают коэффициенты исходной модели. Как показано на рисунке, 10.2A сначала увеличивают, а затем уменьшают В принципе, задержка может быть выражена в виде квадратичной функции. Однако это распределение имеет нежелательные характеристики. Выпуклые на На графике функций масштаб не может быть плавно приближен к нулю.
С этого момента Показана кубическая функция, показанная на рис. 3. 10.3, это имеет два крайних значения. Более привлекательный: встречается около второй экстрима Плавный нисходящий вес. На самом деле, распределение задержек объясняющих переменных может не соответствовать.
Есть простые функции, и если вы попытаетесь их использовать, Нежелательный результат: набрать вес с неправильным знаком, острый Например, снижение веса на краю распределения. Все эти вопросы в принципе Можно преодолеть с помощью полиномов высшего порядка: Sh. аль- Ее статья mon использует полином 4-го порядка, Удовлетворительный результат. Однако, если степень многочлена снова возрастает Существует неизвестный риск мультиколлинеарности.
Количество изменений z равно числу слагаемых в полиноме, а переменные z коррелируют друг с другом Другая причина заключается в том, что каждый из них представляет собой линейную комбинацию тока и тока. Значение лага x. На первый взгляд все еще привлекательно испытать все возможные комбинации.
Полиномиальный порядок и число значений запаздывания Дайте априорное выражение или результат, наиболее близкий к экстремальному значению Наиболее соответствует им. Наконец, вместо предоставления Независимый тест гипотезы «Эксперимент превращается в поиск подтверждения В ожидании априорного выражения. случай.
При построении регрессионно-зависимого уравнения для стоимости жилья По данным 1959 года, из личного дохода и индекса фактических цен на жилье Из таблицы 1983 года было решено использовать приведенную выше схему 6.9 Алмона. (Вторичная функция, период с 3 лагами) переменные дохода и цены.
Уравнение регрессии, которое согласуется с (10.57), постоянный член Вена — 2,33, коэффициент при ZQ, Z {и переменный доход Z2 равны 305 0,417, -0,159 и 0,025 соответственно. Это полином Функция теперь выглядит так: р = 0,417-0,159 * + 0,025 * 2. (10.58) Подставляя значения 0, 1, 2 и 3 этого выражения в s, получаем: Коэффициент текущего значения и значения задержки x: I6g y {= -2,33 + 0,417 log x, + 0,283 log xM + 0,199 log x ^ 2 + + 0,165 log x, _3 + компонент цены. (10.59)
В этом случае фасет квадратичной функции оказался вогнутым вниз. Рисунок 10.2B, и распределение наконечников такое же, как укороченная форма Распределение кроватей. движение 10,11. Коэффициенты ZQ, ZX и Z2 являются переменными ценами в регрессии Формулы стоимости жилья составляли -0,035, 0,249 и -0,165 соответственно. log /? , Log />, , logPf_2 и log / 7 ^ _3 и коэффициенты комментариев вычисляются Проверьте результат.
Смотрите также:
| Частичная корректировка | Рациональные ожидания |
| Адаптивные ожидания | Предсказание |
Если вам потребуется помощь по эконометрике вы всегда можете написать мне в whatsapp.

