Гиперболический параболоид
Исследуем поверхность, определяемую уравнением
где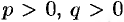 
. Рассечем поверхность (12.34) плоскостями 
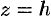. Получим кривую
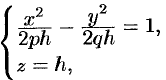
которая при всех значениях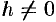 
является гиперболой. При 
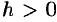ее действительные оси параллельны оси 
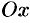, при 
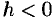— параллельны оси 
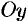, при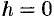 
линия пересечения 
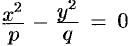распадается на пару пересекающихся прямых 
и 
. При пересечении поверхности плоскостями, параллельными плоскости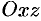 
(
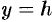), будут получаться параболы
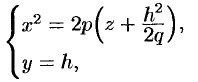
ветви которых направлены вверх. При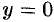 
в сечении получается парабола
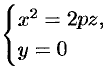
с вершиной в начале координат и осью симметрии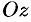 
.
Пересекая поверхность (12.34) плоскостями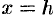 
, получим параболы 
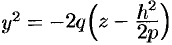, ветви которых направлены вниз.
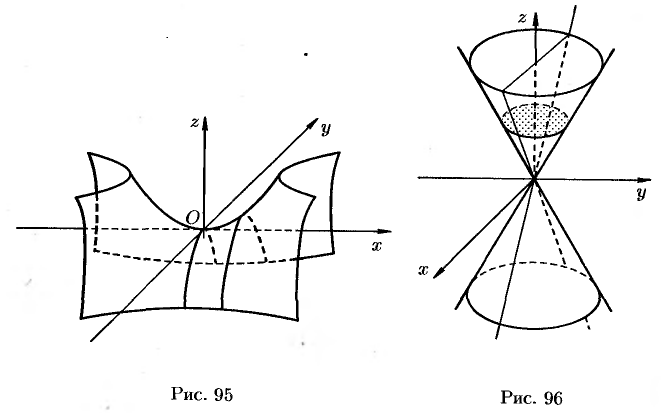
Анализ линии пересечения позволяет определить вид поверхности: опа имеет вид седла (см. рис. 95). Поверхность (12.34) называется гиперболическим параболоидом.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Двухполостный гиперболоид |
| Эллиптический параболоид |
| Конус второго порядка |
| Работа переменной силы в определённом интеграле |
