Гиперболические функции и их производные
В математике, механике, электротехнике и некоторых других дисциплинах встречаются гиперболические функции, определяемые следующими формулами:
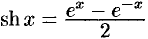 — гиперболический синус;
— гиперболический синус;-
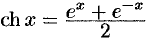 — гиперболический косинус («цепная линия»);
— гиперболический косинус («цепная линия»); -
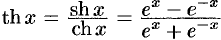 и
и 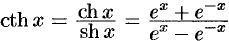 — гиперболический тангенс и котангенс, где
— гиперболический тангенс и котангенс, где 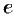 — неперово число.
— неперово число.
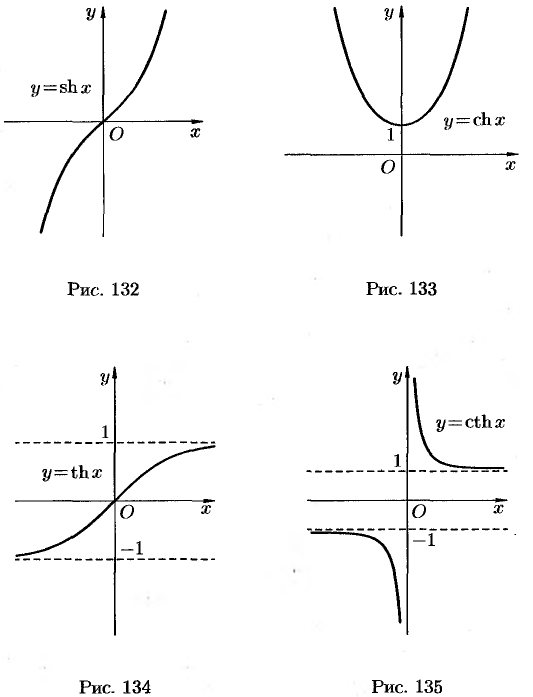
На рисунках 132-135 показаны графики гиперболических функций.
Между гиперболическими функциями существуют следующие основные зависимости:
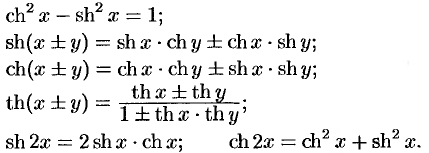
Все эти формулы вытекают из определения гиперболических функций.
Например,
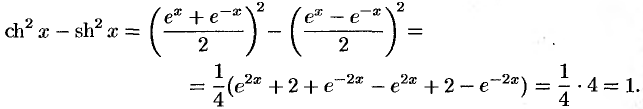
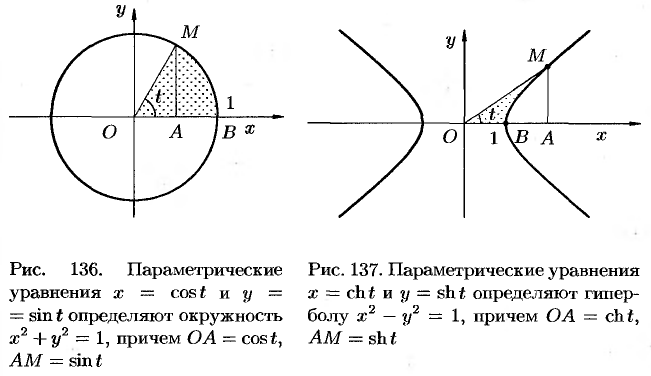
Геометрическая интерпретация гиперболических функций (см. рис. 137) аналогична интерпретации тригонометрических функций (см. рис. 136).
Найдем производные гиперболических функций:
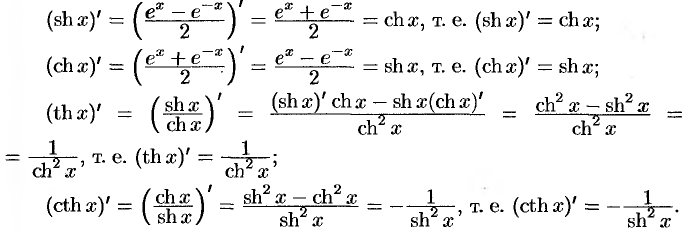
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Производная суммы, разности, произведения и частного функций |
| Производная сложной и обратной функций |
| Правило Лопиталя и раскрытие неопределённостей |
| Раскрытие неопределенностей различных видов |

